Nội dung từ Loigiaihay.Com
Cho hàm số $y = \dfrac{{x - 2}}{{{x^2} - 2x + m}}\left( C \right).$ Tất cả các giá trị của m để (C) có 3 đường tiệm cận là:
-
A.
$m < 1$
-
B.
$m \ne 0$
-
C.
$m = - 3$
-
D.
$m < 1;\,m \ne 0$
- Tìm tiệm cận ngang của đồ thị hàm số.
- Nêu điều kiện để đồ thị hàm số có 3 tiệm cận là nó phải có 2 tiệm cận đứng.
$y = \dfrac{{x - 2}}{{{x^2} - 2x + m}}$
$\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{x - 2}}{{{x^2} - 2x + m}} = \mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{\dfrac{1}{x} - \dfrac{2}{{{x^2}}}}}{{1 - \dfrac{2}{x} + \dfrac{m}{{{x^2}}}}} = 0 $
Suy ra $y = 0$ là tiệm cận ngang của đồ thị hàm số
Để đồ thị hàm số có 3 đường tiệm cận $\Leftrightarrow $ Đồ thị hàm số phải có hai đường tiệm cận đứng
$ \Leftrightarrow {x^2} - 2x + m = 0$ có 2 nghiệm phân biệt khác $2$
$ \Leftrightarrow \left\{ \begin{gathered} \Delta ' > 0 \hfill \\ {2^2} - 2.2 + m \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 1 - m > 0 \hfill \\ m \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 1 \hfill \\ m \ne 0 \hfill \\ \end{gathered} \right.$
Đáp án : D

Các bài tập cùng chuyên đề
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{x - 1}}{{ - 3x + 2}}\) là?
Đường thẳng $y = {y_0}$ là tiệm cận ngang của đồ thị hàm số $y = f\left( x \right)$ nếu:
Cho hàm số \(y = \dfrac{{x - 2}}{{x + 2}}\) có đồ thị \((C)\). Tìm tọa độ giao điểm \(I\) của hai đường tiệm cận của đồ thị \((C)\)
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{2x + c}}\) có tiệm cận ngang \(y = 2\) và tiệm cận đứng \(x = 1\) thì \(a + c\) bằng
Cho hàm số \(y = \dfrac{{2018}}{{x - 2}}\) có đồ thị \(\left( H \right).\) Số đường tiệm cận của \(\left( H \right)\) là:
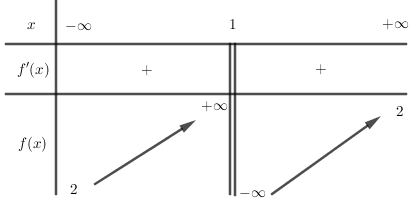
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
Số tiệm cận ngang của đồ thị hàm số \(y = 2x - 1 + \sqrt {4{x^2} - 4} \) là
Tất cả phương trình tiệm cận ngang của đồ thị hàm số $y = \dfrac{{\sqrt {{x^2} + x + 1} }}{{2x + 3}}$ là:
Đồ thị hàm số $y = \dfrac{x}{{\sqrt {{x^2} - 1} }}$ có bao nhiêu đường tiệm cận ngang:
Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 4}}{{{x^2} - 16}}$ là:
Đồ thị hàm số $y = \dfrac{{x - 3}}{{{x^2} + x - 2}}$ có bao nhiêu đường tiệm cận đứng?
Số đường tiệm cận của đồ thị hàm số $y = \dfrac{{x - 1}}{{2 - x}}$ là:
Cho hàm số $y = \dfrac{{3x}}{{1 + 2x}}$. Khẳng định nào sau đây là khẳng định đúng?
Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng $d:y = x$?
Phương trình đường tiệm cận xiên của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 1}}{{x + 1}}$ là:
Đồ thị hàm số \(y = \sqrt {4{x^2} + 4x + 3} - \sqrt {4{x^2} + 1} \) có bao nhiêu đường tiệm cận ngang?
Cho hàm số $y = \dfrac{{2mx + m}}{{x - 1}}\left( C \right).$. Với giá trị nào của $m \left({m\ne0}\right)$ thì đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng $8$?
Cho hàm số $y = \dfrac{{2{x^2} - 3{x} + m}}{{x - m}}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số $m$ là:












