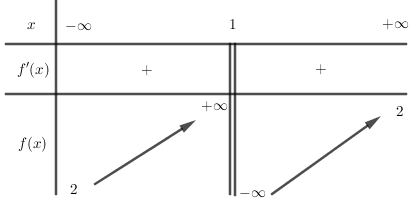
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y =  + \infty$ thì đường thẳng $x = {x_0}$ là:

Tiệm cận ngang của đồ thị hàm số $y = \dfrac{{x - 1}}{{ - 3x + 2}}$ là?

Đường thẳng $y = {y_0}$ là tiệm cận ngang của đồ thị hàm số $y = f\left( x \right)$ nếu:

Cho hàm số $y = \dfrac{{x - 2}}{{x + 2}}$ có đồ thị $(C)$. Tìm tọa độ giao điểm $I$ của hai đường tiệm cận của đồ thị $(C)$

Đồ thị hàm số $y = \dfrac{{ax + b}}{{2x + c}}$ có tiệm cận ngang $y = 2$ và tiệm cận đứng $x = 1$ thì $a + c$ bằng

Cho hàm số $y = \dfrac{{2018}}{{x - 2}}$ có đồ thị $\left( H \right).$ Số đường tiệm cận của $\left( H \right)$ là:

Đồ thị hàm số nào sau đây có 3 đường tiệm cận?

Số tiệm cận ngang của đồ thị hàm số $y = 2x - 1 + \sqrt {4{x^2} - 4}$ là

Tất cả phương trình tiệm cận ngang của đồ thị hàm số $y = \dfrac{{\sqrt {{x^2} + x + 1} }}{{2x + 3}}$ là:

Đồ thị hàm số $y = \dfrac{x}{{\sqrt {{x^2} - 1} }}$ có bao nhiêu đường tiệm cận ngang:

Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 4}}{{{x^2} - 16}}$ là:

Đồ thị hàm số $y = \dfrac{{x - 3}}{{{x^2} + x - 2}}$ có bao nhiêu đường tiệm cận đứng?

Số đường tiệm cận của đồ thị hàm số $y = \dfrac{{x - 1}}{{2 - x}}$ là:

Cho hàm số $y = \dfrac{{3x}}{{1 + 2x}}$. Khẳng định nào sau đây là khẳng định đúng?

Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng $d:y = x$?

Phương trình đường tiệm cận xiên của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 1}}{{x + 1}}$ là:

Đồ thị hàm số $y = \sqrt {4{x^2} + 4x + 3}  - \sqrt {4{x^2} + 1}$ có bao nhiêu đường tiệm cận ngang?

Cho hàm số $y = \dfrac{{2mx + m}}{{x - 1}}\left( C \right).$. Với giá trị nào của $m \left({m\ne0}\right)$ thì đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng $8$?

Cho hàm số $y = \dfrac{{x - 2}}{{{x^2} - 2x + m}}\left( C \right).$ Tất cả các giá trị của m để (C) có 3 đường tiệm cận là:

Cho hàm số $y = \dfrac{{2{x^2} - 3{x} + m}}{{x - m}}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số $m$ là: