Lý thuyết Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12 Cánh Diều1. Định nghĩa Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa 1. Định nghĩa
2. Ý nghĩa
Ví dụ: Anh An đầu tư số tiền bằng nhau vào hai lĩnh vực kinh doanh A, B. Anh An thống kê số tiền thu được mỗi tháng trong vòng 60 ngày theo mỗi lĩnh vực có kết quả như sau:
So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực A, B. Đầu tư vào lĩnh vực nào “rủi ro” hơn? Giải: Chọn giá trị đại diện cho các nhóm số liệu ta có:
Số tiền trung bình thu được khi đầu tư vào các lĩnh vực A, B tương ứng là: \(\overline {{x_A}} = \frac{1}{{60}}(5.7,5 + ... + 5.27,5) = 17,5\) (triệu đồng) \(\overline {{x_B}} = \frac{1}{{60}}(20.7,5 + ... + 20.27,5) = 17,5\) (triệu đồng) Như vậy, về trung bình đầu tư vào các lĩnh vực A, B số tiền thu được hàng tháng như nhau. Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực A, B tương ứng là: \({s_A} = \sqrt {\frac{1}{{60}}(5.7,{5^2} + ... + 5.27,{5^2} - 17,{5^2}} = 5\) \({s_B} = \sqrt {\frac{1}{{60}}(20.7,{5^2} + ... + 20.27,{5^2} - 17,{5^2}} \approx 8,42.\) Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực B cao hơn khi đầu tư vào lĩnh vực A. Người ta nói rằng, đầu tư vào lĩnh vực B là “rủi ro” hơn. 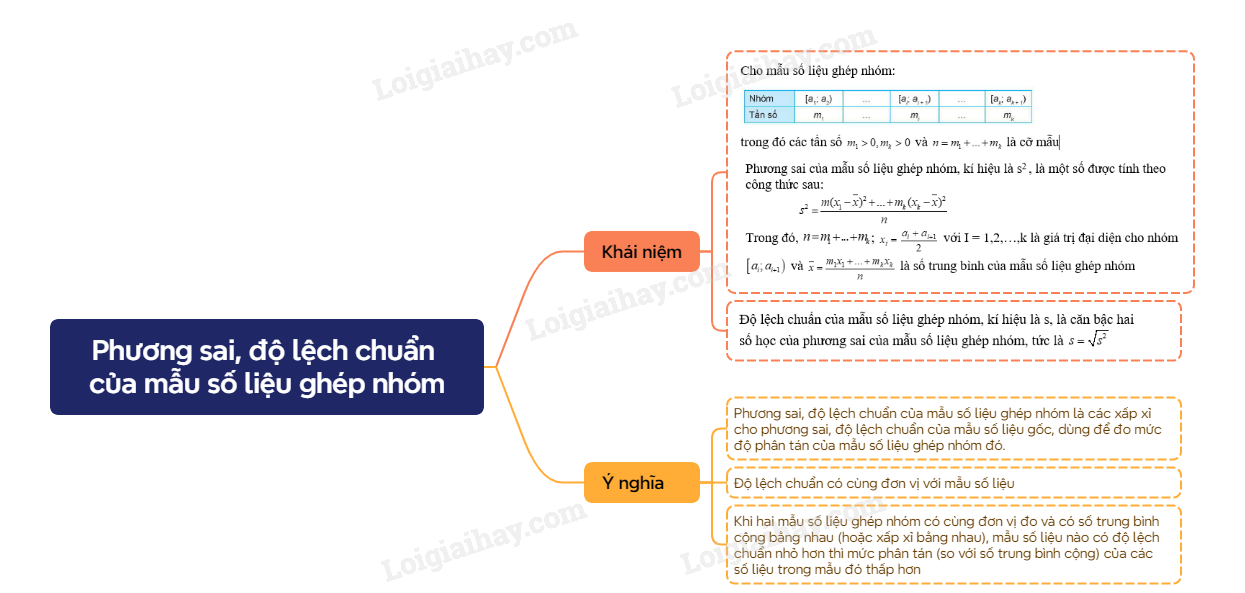
|