Lý thuyết Hàm số y = ax² (a ≠ 0) Toán 9 Chân trời sáng tạo

1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Ví dụ: Hàm số \(y = 2{x^2},y =  - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).

2. Bảng giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Để lập bảng giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta lần lượt cho x nhận các giá trị \({x_1},{x_2},{x_3},...\) (\({x_1},{x_2},{x_3},...\) tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng sau:

Ví dụ: Bảng giá trị của hàm số \(y = {x^2}\):

Nhận xét: Với hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta có:

- Nếu \(a > 0\) thì \(y > 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).

- Nếu \(a < 0\) thì \(y < 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).

3. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).

Bảng giá trị của hàm số:

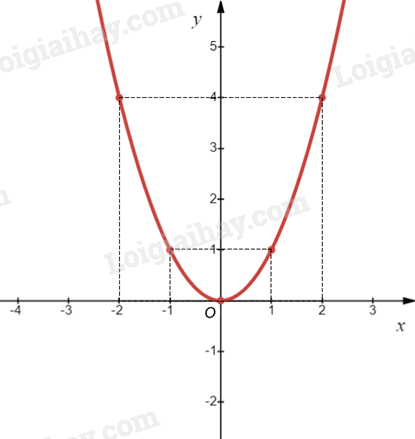
Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:

Nhận xét