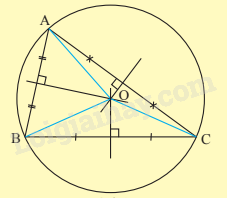
Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Cùng khám phá1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác – Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn. – Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. Bán kính của đường tròn ngoại tiếp tam giác là khoảng cách từ giao điểm này đến một đỉnh bất kì của tam giác. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh 1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác
Ví dụ:
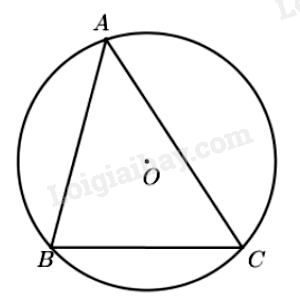
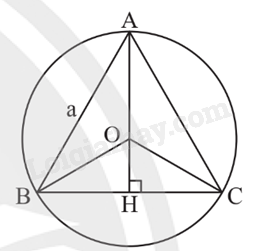
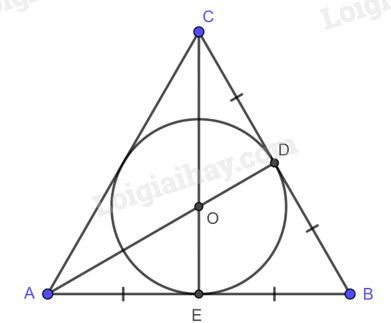
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O). - Tâm O là giao điểm của ba đường trung trực của tam giác ABC. Đường tròn ngoại tiếp tam giác vuông
Ví dụ:
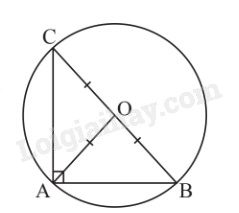
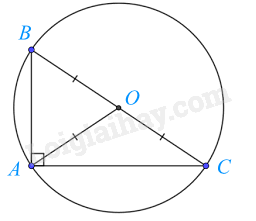
Tam giác ABC nội tiếp đường tròn (O; BO). Đường tròn ngoại tiếp tam giác đều
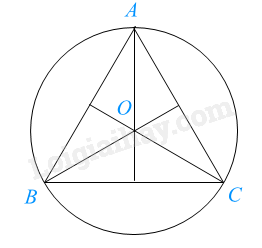
Ví dụ:
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\). 2. Đường tròn nội tiếp một tam giác Định nghĩa đường tròn nội tiếp tam giác
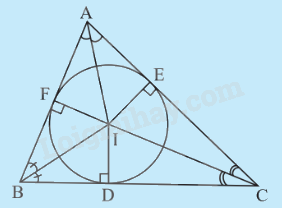
Ví dụ:
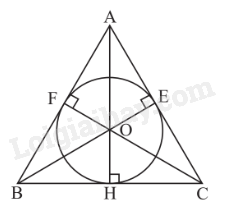
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I). - Tâm I là giao điểm của ba đường phân giác của tam giác. Đường tròn nội tiếp tam giác đều
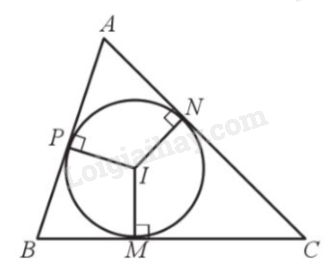
Ví dụ: Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\). 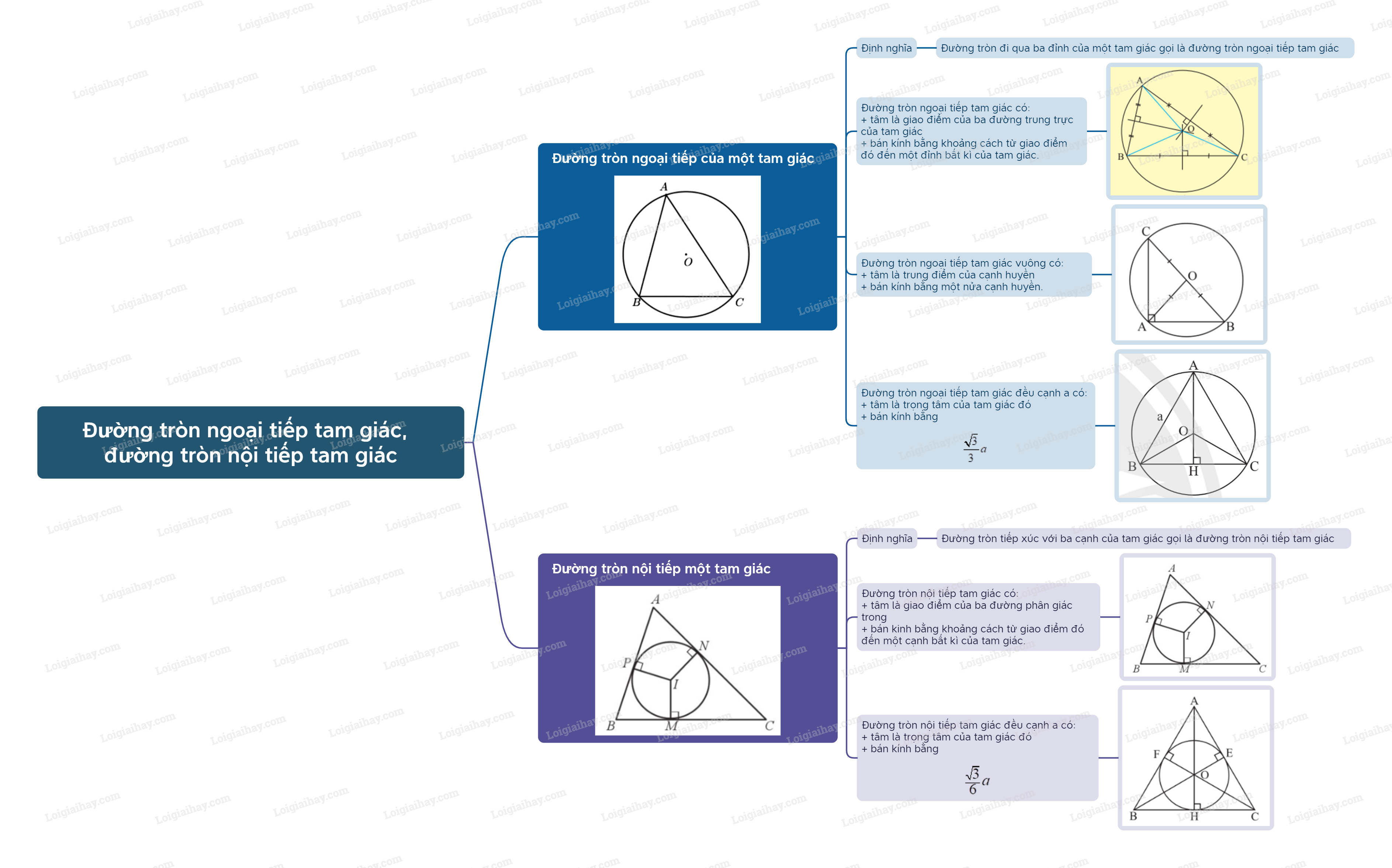
|