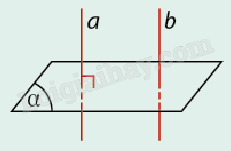
Lý thuyết Đường thẳng vuông góc với mặt phẳng. Phép chiếu vuông góc - SGK Toán 11 Cùng khám phá

A. Lý thuyết

1. Đường thẳng vuông góc với mặt phẳng

a) Khái niệm

b) Điều kiện để một đường thẳng vuông góc với một mặt phẳng

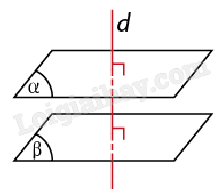
2. Tính chất của quan hệ vuông góc giữa đường thẳng và mặt phẳng

a) Sự tồn tại của các đường thẳng và mặt phẳng vuông góc với nhau

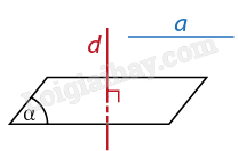
Lưu ý:

- Mặt phẳng qua trung điểm M của đoạn thẳng AB và vuông góc với đường thẳng AB gọi là mặt phẳng trung trực của đoạn thẳng AB.

- Mặt phẳng trung trực của một đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng này.

b) Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng

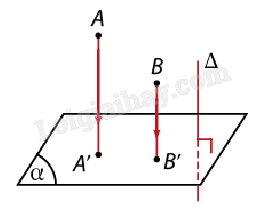
3. Phép chiếu vuông góc. Định lí ba đường vuông góc

a) Phép chiếu vuông góc

Nhận xét:

- Nếu phép chiếu vuông góc lên mặt phẳng \((\alpha )\) còn được gọi đơn giản là phép chiếu lên mặt phẳng \((\alpha )\). Nếu H’ là hình chiếu vuông góc của H lên mặt phẳng

\((\alpha )\) thì ta cùng nói H’ là hình chiếu của H trên mặt phẳng \((\alpha )\).

- Phép chiếu vuông góc cũng có mọi tính chất của phép chiếu song song.

b) Định lí ba đường vuông góc

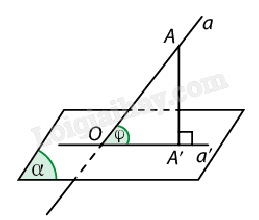
4. Góc giữa đường thẳng và mặt phẳng

Lưu ý: Gọi \(\varphi \) là góc giữa đường thẳng a và mặt phẳng (α), ta có:

+ \({0^o} < \varphi  < {90^o}\).

+ a // (α) hoặc \(a \subset (\alpha )\) thì \(\varphi  = {0^o}\).

+ \(a \bot (\alpha ) \Leftrightarrow \varphi  = {90^o}\).

B. Bài tập

Bài 1: Trong không gian, cho tam giác ABC và đường thẳng d vuông góc với AB và AC. Chứng minh d vuông góc với BC.

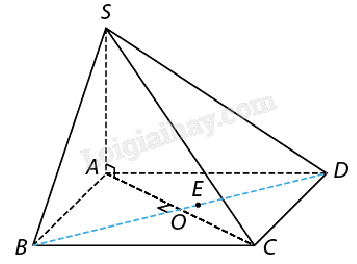
Giải:

Theo giả thiết: \(d \bot AB\); \(d \bot AC\). Hai đường thẳng AB và AC cắt nhau, tạo nên mặt phẳng (ABC). Áp dụng định lí trên, ta có \(d \bot (ABC)\). Mà \(BC \subset (ABC)\), nên \(d \bot BC\).

Bài 2: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và ABCD là hình vuông có O là giao điểm hai đường chéo.

a) Chứng minh rằng (SAC) là mặt phẳng trung trực của đoạn thẳng BD.

b) Gọi E là một điểm trong không gian sao cho DE ⊥ (SAC). Chứng minh B, D, E thẳng hàng.

c) c) Giả sử (α) là mặt phẳng qua S vuông góc với BD. Hãy xác định giao tuyến của hai mặt phẳng (α) và (ABCD).

Giải:

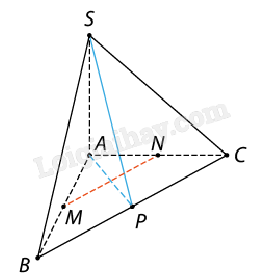
a) Vì SA ⊥ (ABCD) nên BD ⊥ (SAC).

Ta lại có: BD ⊥ AC (do ABCD là hình vuông). Suy ra BD ⊥ (SAC).

b) Ta có: BD và DE cùng vuông góc với (SAC).

Do qua D có duy nhất một đường thẳng vuông góc với (SAC) nên các đường thẳng BD và DE phải trùng nhau. Điều đó có nghĩa là B, D, E thẳng hàng.

c) Ta đã chứng minh được BD ⊥ (SAC). Mặt khác, chỉ có một mặt phẳng qua S và vuông góc với BD, đó là mặt phẳng (SAC). Vậy mặt phẳng (α) chính là (SAC).

Suy ra giao tuyến của (α) và (ABCD) là AC.

Bài 3: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC cân tại A. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Chứng minh MN và BC cùng vuông góc với mặt phẳng (SAP).

Giải:

ΔABC cân tại A, P là trung điểm của BC, do đó BC ⊥ AP.

SA ⊥ (ABC) nên SA ⊥ BC. Suy ra BC ⊥ (SAP).

Mà MN // BC (đường trung bình của tam giác BAC) nên hai đường thẳng BC, MN cùng vuông góc với mặt phẳng (SAP).

Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng đáy. Gọi N, M lần lượt là trung điểm của các cạnh SD, AD. Mặt phẳng (α) qua MN và song song với AC. Chứng minh BD vuông góc mặt phẳng (α).

Giải:

Ta có MN // SA (đường trung bình trong tam giác SAD) ⇒ (α) // SA, mà (α) // AC nên (α) // (SAC).

Ta có BD ⊥ SA (SA ⊥ (ABCD)) và BD ⊥ AC (hai đường chéo hình vuông) nên BD ⊥ (SAC).

Vậy BD ⊥ (α).

Bài 5: Cho mặt phẳng (α) và tam giác OAB vuông tại O có cạnh OA // (α), cạnh OB không vuông góc với (α). Qua O, A, B lần lượt vẽ đường thẳng d, a, b vuông góc với (α) và cắt (α) lần lượt tại O', A', B'. Chứng minh tam giác O'A'B' vuông tại O'.

Giải:

Ta có: OA // (α), OO' ⊥ (α) nên OO' ⊥ OA.

Mà OA ⊥ OB nên A ⊥ (OO'B') (OO' // BB' vì cùng vuông góc với (α)).

Do OA // (α), (OO'A) ∩ (α) = O'A' ⊥ OA.

Vậy O'A' ⊥ (OO'B') nên O'A' ⊥ O'B' hay tam giác O'A'B' vuông tại O'.

Bài 6: Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với đáy (ABCD). Xác định hình chiếu của:

a) Đường thẳng SA trên mặt phẳng (ABCD).

b) Cạnh SC trên mặt phẳng (ABCD).

c) Tam giác SBD trên mặt phẳng (ABCD).

Giải:

a) Theo giả thiết, SA ⊥ (ABCD) nên hình chiếu của đường thẳng SA trên mặt phẳng (ABCD) là điểm A.

b) C ∈ (ABCD) nên hình chiếu của C trên mặt phẳng (ABCD) chính là C. Mặt khác, hình chiếu của S trên (ABCD) là điểm A. Suy ra, hình chiếu của cạnh SC trên (ABCD) là AC.

c) Hình chiếu của B, D trên (ABCD) lần lượt là chính B, D. Hình chiếu của S trên (ABCD) là A.

Suy ra, hình chiếu của ΔSBD trên (ABCD) là ΔABD.

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và SA vuông góc với mặt phẳng đáy. Chứng minh rằng ABCD là hình thoi khi và chỉ khi BD vuông góc với SC.

Giải:

Theo giả thiết, SA ⊥ (ABCD) nên hình chiếu của S trên mặt phẳng (ABCD) là A. Vì C ∈ (ABCD) nên hình chiếu của C là chính nó. Vậy hình chiếu của cạnh SC là AC.

Từ đó suy ra:

- Nếu ABCD là hình thoi thì BD ⊥ SC. Do đó, BD ⊥ SC.

- Ngược lại, nếu SC ⊥ BD vuông góc với hình chiếu của SC, nghĩa là BD ⊥ AC. Khi đó, hình bình hành ABCD có hai đường chéo vuông góc với nhau. Suy ra ABCD là hình thoi.

Bài 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), SA = \(a\sqrt 2 \). Xác định và tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

Giải:

Ta có SA vuông góc với mặt phẳng (ABCD) tại A, nên AC là hình chiếu của SC trên mặt phẳng (ABCD).

Vậy góc giữa SC và mặt phẳng (ABCD) là góc giữa SC và AC. Đó là \(\widehat {SCA}\).

Ta có \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{\sqrt 2 a}}{{\sqrt 2 a}} = 1\). Suy ra \(\widehat {SCA} = {45^o}\).

Vậy góc giữa SC và mặt phẳng (ABCD) là \(\widehat {SCA} = {45^o}\).