Giải mục 4 trang 62 SGK Toán 11 tập 2 - Cùng khám phá

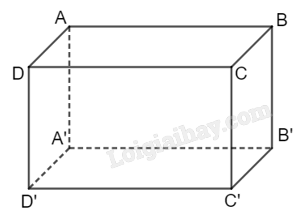
Hoạt động 6

Cho hình hộp $ABCD.A'B'C'D'$ có $AA' \bot \left( {ABCD} \right)$.

a) Tìm hình chiếu $d$ của $A'C$ trên mặt phẳng $\left( {ABCD} \right)$. Xác định góc giữa $A'C$ và $d$

b) Tìm hình chiếu $a$ của $A'C'$ trên mặt phẳng $\left( {ABCD} \right)$. Xác định góc giữa $A'C'$ và $a$

Phương pháp giải:

a) Chứng minh $A'A \bot \left( {ABCD} \right)$ từ đó suy ra $A'$ là hình chiếu của $A$ trên $\left( {ABCD} \right)$

b) Chứng minh $CC' \bot \left( {ABCD} \right)$ từ đó suy ra $C'$ là hình chiếu của $C$ trên $\left( {ABCD} \right)$

Lời giải chi tiết:

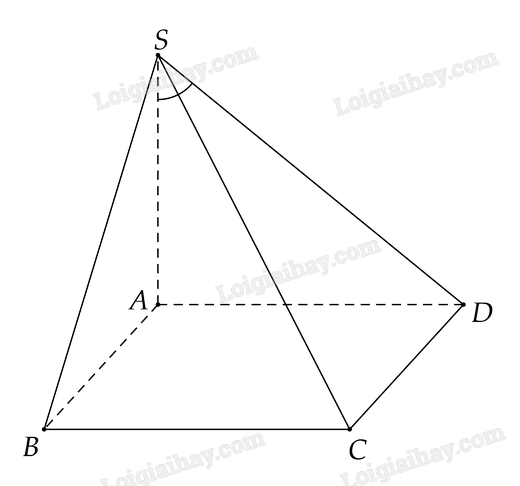
a) Vì $A'A \bot \left( {ABCD} \right)$ nên $A$ là hình chiếu của $A'$ trên $\left( {ABCD} \right)$

Vậy hình chiếu $d$ của $A'C$ trên $\left( {ABCD} \right)$ là $AC$

Góc giữa $A'C$ và $AC$ là góc $\widehat {A'CA}$

b) Vì $A'A \bot \left( {ABCD} \right)$ nên $A$ là hình chiếu của $A'$ trên $\left( {ABCD} \right)$

Vì $CC' \bot \left( {ABCD} \right)$ nên $C$ là hình chiếu của $C'$ trên $\left( {ABCD} \right)$

Vậy hình chiếu $a$ của $A'C'$ trên $\left( {ABCD} \right)$ là $AC$

Vì $A'C'//AC$ nên góc giữa $A'C'$ và $AC$ bằng ${0^o}$

Quảng cáo

Luyện tập 8

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$, $SA = a\sqrt 3$. Xác định và tính góc giữa đường thẳng $SD$ và $\left( {SAB} \right)$

Phương pháp giải:

Xác định giao điểm $S$ của $SD$ và $\left( {SAB} \right)$

Chứng minh $DA \bot \left( {SAB} \right)$ từ đó suy ra $SA$ là hình chiếu vuông góc của $SD$ trên $\left( {SAB} \right)$ suy ra góc cần tìm là góc giữa 2 đường thẳng $SD$ và $SA$

Sử dụng tỉ số lượng giác trong tam giác vuông

Lời giải chi tiết:

Ta có $S$ là giao điểm của $SD$ và $\left( {SAB} \right)$ $\left( 1 \right)$

Vì $SA \bot \left( {ABCD} \right)$ nên $SA \bot AD$.

Vì $ABCD$ là hình vuông lên $AD \bot AB$

Ta có $\left\{ \begin{array}{l}AD \bot SA\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow$$A$ là hình chiếu vuông góc của $D$ trên $\left( {SAB} \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra  $SA$ là hình chiếu vuông góc của $SD$ trên $\left( {SAB} \right)$

Vậy góc giữa $SD$ và $\left( {SAB} \right)$ là góc giữa $SA$ và $SD$ là góc giữa $\widehat {DSA}$

Xét $\Delta SAD$ vuông tại $A$ có $\tan S = \frac{{AD}}{{SA}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {ASD} = {30^o}$