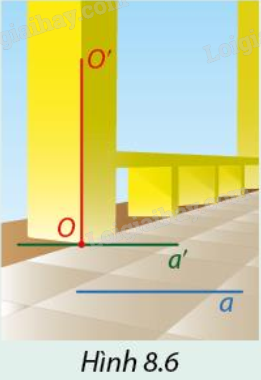
Giải mục 1 trang 55, 56 SGK Toán 11 tập 2 - Cùng khám phá

Hoạt động 1

Quan sát hình ảnh cây cột và nền nhà (Hình 8.6). Xem nền nhà là hình ảnh của mặt phẳng \(\left( \alpha  \right)\). Ta có cạnh \(OO'\) của cây cột tượng trưng cho một đường thẳng với \(O\) tượng trưng cho một điểm thuộc \(\left( \alpha  \right)\)

a) Vẽ một đường thẳng \(a\) nằm trong \(\left( \alpha  \right)\) và \(a\) không đi qua \(O\). Vẽ đường thẳng \(a'\) qua \(O\) và song song với \(a\). Dùng ê ke kiểm tra \(OO'\) có vuông góc với đường thẳng \(a'\) hay không? Từ đó hãy tính góc giữa \(OO'\) và \(a\).

b) Gọi \(d\) là đường thẳng bất kì nằm trong \(\left( \alpha  \right)\). Hỏi \(OO'\) có vuông góc với \(d\) không? Vì sao?

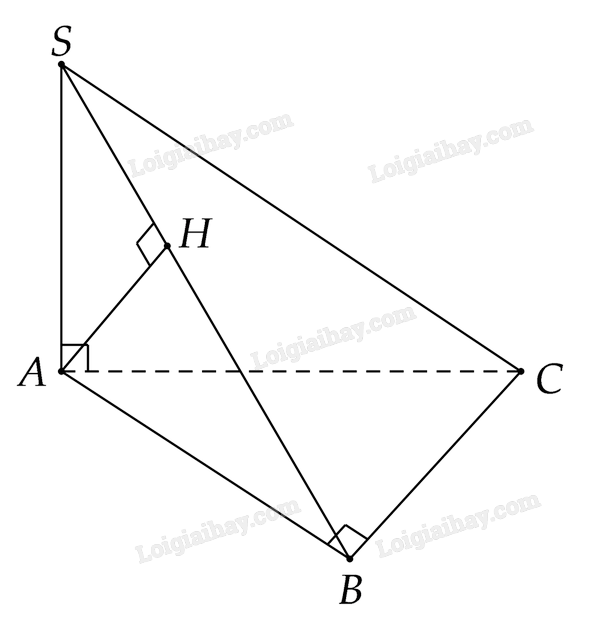
Phương pháp giải:

Để dùng eke kiểm tra vuông góc ta đặt cạnh của eke trùng với \(OO'\), nếu cạnh eke còn lại trùng với đường thẳng \(a\) thì \(OO'\) vuông góc với \(a\)

Lời giải chi tiết:

a) \(OO'\) có vuông góc với đường thẳng \(a\). Góc giữa \(OO'\) và đường thẳng \(a\) bằng \({90^o}\)

b) \(OO'\) vuông góc với \(d\) vì \(OO'\) vuông góc với \(\left( \alpha  \right)\)

Luyện tập 1

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và tam giác \(ABC\) vuông tại \(B\).

a) Chứng minh rằng \(BC\) vuông góc với mặt phẳng \(\left( {SAB} \right)\)

b) Biết \(AH\) là đường cao của tam giác \(SAB\). Chứng minh \(AH\) vuông góc với \(SC\)

Phương pháp giải:

a) Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

Chứng minh \(BC\) vuông góc với \(SA\) và \(AB\)

b) Chứng minh \(AH\) vuông góc với \(BC\) và \(SB\)

Lời giải chi tiết:

a) Ta có \(BC \bot AB\) vì \(\Delta ABC\) vuông tại \(B\)

Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)

Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\SA \cap AB = \left\{ A \right\}\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)

b) Ta có \(\left\{ \begin{array}{l}BC \bot \left( {SAB} \right)\\AH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow BC \bot AH\)

Vì \(AH\) là đường cao của tam giác \(SAB\) \( \Rightarrow AH \bot SB\)

Ta có \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\)