Giải mục 2 trang 56, 57, 58, 59, 60 SGK Toán 11 tập 2 - Cùng khám pháCho hình hộp ABCD.A′B′C′D′ có AA′⊥AB và A′A⊥AD (Hình 8.8)
Lựa chọn câu để xem lời giải nhanh hơn
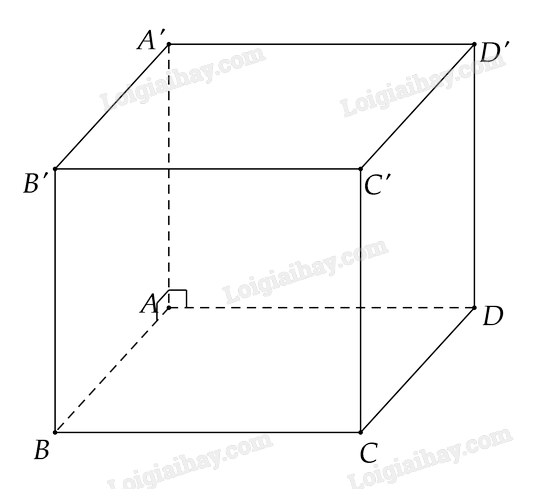
Hoạt động 2 Cho hình hộp ABCD.A′B′C′D′ có AA′⊥AB và A′A⊥AD (Hình 8.8) a) Mặt phẳng (ABCD) có vuông góc với A′A không? Vì sao? b) Gọi (α) là mặt phẳng qua A và vuông góc với A′A. Hãy tìm giao tuyến của (α) với các mặt phẳng (AA′B′B) và (A′ADD′). Từ đó tìm mối quan hệ giữa (α) và mặt phẳng (ABCD) Phương pháp giải: a) Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy. b) Tìm 2 điểm chung của 2 mặt phẳng là ta tìm được giao tuyến của chúng. Lời giải chi tiết:
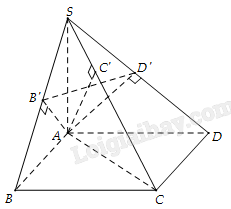
a) Vì {AA′⊥ABAA′⊥ADAB∩AD={A}⇒AA′⊥(ABCD) b) Vì (α) đi qua A và vuông góc với AA′⇒(α) trùng với (ABCD) Do đó (α)∩(AA′B′B)=AB (α)∩(AA′D′D)=AD Luyện tập 2 Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA vuông góc với đáy. Gọi B′,C′,D′ lần lượt là hình chiếu của A trên các cạnh SB,SC,SD. Chứng minh SC⊥(AB′D′) và AB′,AC′,AD′ cùng nằm trên một mặt phẳng. Phương pháp giải: Chứng minh AB′⊥(SBC)⇒AB′⊥SC Chứng minh AD′⊥(SCD)⇒AD′⊥SC Chứng minh ba đường thẳng AB′,AC′,AD′ cùng vuông góc với một đường thẳng Lời giải chi tiết:
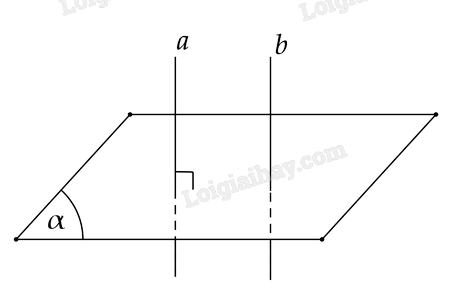
+) Ta có BC⊥AB (Vì ABCD là hình chữ nhật) BC⊥SA vì SA⊥(ABCD) Vì {BC⊥ABBC⊥SA⇒BC⊥(SAB) Mà AB′⊂(SAB)⇒AB′⊥BC Vì {AB′⊥SBAB′⊥BC⇒AB′⊥(SBC)⇒AB′⊥SC +) Ta có DC⊥AD (Vì ABCD là hình chữ nhật) DC⊥SA vì SA⊥(ABCD) Vì {DC⊥ADDC⊥SA⇒DC⊥(SAD) Mà AD′⊂(SAD)⇒AD′⊥DC Vì {AD′⊥SDAD′⊥DC⇒AD′⊥(SDC)⇒AD′⊥SC Vì {SC⊥AB′SC⊥AD′⇒SC⊥(AB′D′) +) Ta có AB′,AC′,AD′ cùng vuông góc với SC suy ra chúng cùng nằm trên mặt phẳng. Mà SC⊥(AB′D′) nên mặt phẳng đó là (AB′D′) Hoạt động 3 Cho hai đường thẳng a,b song song với nhau và mặt phẳng (α) vuông góc với a (Hình 8.13). Hỏi (α) có vuông góc với b không? Vì sao?
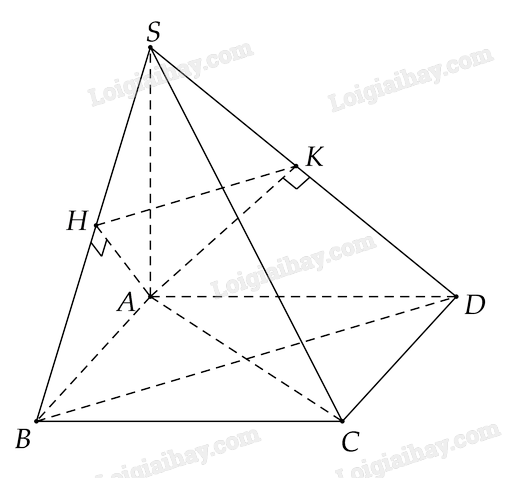
Phương pháp giải: Sử dụng từ vuông góc đến song song Lời giải chi tiết: Ta có {a//ba⊥(α)⇒b⊥(α) Luyện tập 3 Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy. Gọi H,K lần lượt là hình chiếu của A trên SB,SD. Chứng minh HK⊥(SAC) Phương pháp giải: Chứng minh BD⊥(SAC) và HK//BD. Từ đó suy ra HK⊥(SAC) Lời giải chi tiết:
Ta có BD⊥AC (vì ABCD là hình vuông) BD⊥SA vì SA⊥(ABCD) Ta có {BD⊥ACBD⊥SA⇒BD⊥(SAC) (1) Xét ΔSAB có AH⊥SB⇒SHSB=SH.SBSB2=SA2SB2 Xét ΔSAD có AK⊥SD⇒SKSD=SK.SDSD2=SA2SD Mà SB=SD⇒SHSB=SKSD⇒HK//BD (áp dụng định lí Ta – lét) (2) Từ (1) và (2), suy ra HK⊥(SAC) Luyện tập 4 Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và DB, SA=SC, SB=SD. Gọi I,K lần lượt là trung điểm của AB và BC. Mặt phẳng (α) chứa IK và song song với SO. Chứng minh (α)⊥BD Phương pháp giải: Chứng minh (α)//(SAC) Chứng minh BD⊥(SAC) từ đó suy ra BD⊥(α) Lời giải chi tiết:
Ta có IK//AC vì IK là đường trung bình của ΔSAC{IK//ACIK⊂(α)⇒AC//(α) Vì {SO//(α)AC//(α)⇒(SAC)//(α) Vì ABCD là hình thoi tâm O nên AC⊥BD tại O Xét ΔSBD có SB=SD và O là trung điểm của BD⇒SO⊥BD Vì {BD⊥ACBD⊥SO⇒BD⊥(SAC) Mà (α)//(SAC)⇒(α)⊥BD Luyện tập 5 Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA⊥(ABCD). Gọi O là giao điểm của AC và BD, B′ là hình chiếu của A trên SB, O′ là hình chiếu của O trên SC. Chứng minh AB′//(O′BD) Phương pháp giải: AB′//(O′BD) Lời giải chi tiết:
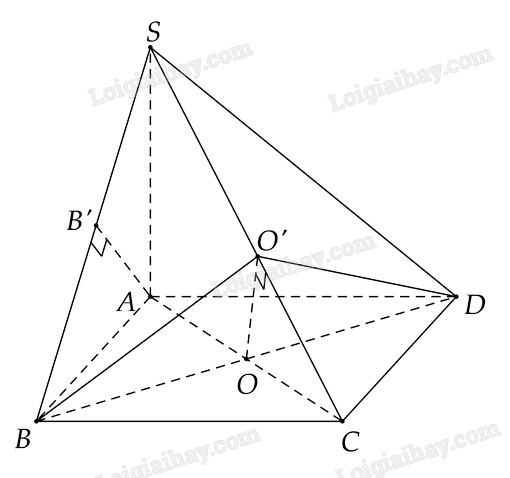
Ta có AC⊥BD (giả thiết) Vì SA⊥(ABCD)⇒SA⊥BD Vì {BD⊥ACBD⊥SA⇒BD⊥(SAC)⇒BD⊥SC Vì {OO′⊥SC(gt)BD⊥SC⇒SC⊥(O′BD) +) Ta có {BC⊥AB(gt)BC⊥SA⇒BC⊥(SAB)⇒BC⊥AB′ Ta có {AB′⊥BCAB′⊥SB⇒AB′⊥(SBC)⇒AB′⊥SC Vì {AB′⊥SC(O′BD)⊥SC⇒AB′//(O′BD)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|