Lý thuyết các trường hợp bằng nhau của tam giác vuông1. Các trường hợp bằng nhau đã biết của hai tam giác vuông. - Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác I. Các kiến thức cần nhớ 1. Nhắc lại các trường hợp bằng nhau đã biết + Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh-góc-cạnh).  + Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (góc-cạnh-góc).  + Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh huyền - góc nhọn) 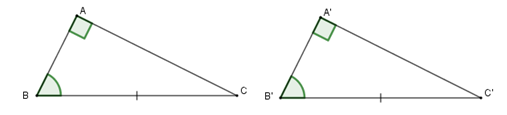 2. Trường hợp bằng nhau cạnh huyền và cạnh góc vuông Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau. Ví dụ: ˆA=^A′=900BC=B′C′AC=A′C′}⇒ΔABC=ΔA′B′C′(ch.cgv) 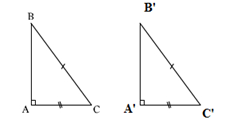 II. Các dạng toán thường gặp Dạng 1: Tìm hoặc chứng minh hai tam giác vuông bằng nhau Phương pháp: - Xét hai tam giác vuông - Kiểm tra các điều kiện bằng nhau cạnh-góc-cạnh, góc-cạnh-góc, cạnh huyền-góc nhọn, cạnh huyền-cạnh góc vuông. - Kết luận hai tam giác bằng nhau Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc. Phương pháp: + Chọn hai tam giác vuông có các yếu tố cần tính hoặc chứng minh. + Chứng minh hai tam giác vuông đó bằng nhau theo một trong các trường hợp đã học + Suy ra các cạnh (góc) tương ứng bằng nhau và kết luận.
|













