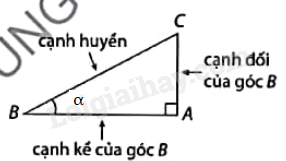
Lý thuyết Các tỉ số lượng giác của góc nhọn Toán 9 Cùng khám phá

1. Khái niệm tỉ số lượng giác của một góc nhọn

Tip học thuộc nhanh:

Lưu ý:

1. Trong một tam giác vuông, độ dài các cạnh luôn là số dương và cạnh góc vuông luôn nhỏ hơn cạnh huyền. Do đó sin và côsin của một góc nhọn luôn dương và nhỏ hơn 1.

\(\alpha  < {90^0}:0 < \sin \alpha  < 1;0 < \cos \alpha  < 1\).

2. Khi ghi các tỉ số lượng giác của một góc nhọn trong tam giác, ta viết \(\sin A\) thay vì \(\sin \widehat A\).

3. \(\cot \alpha  = \frac{1}{{\tan \alpha }}\).

Ví dụ:

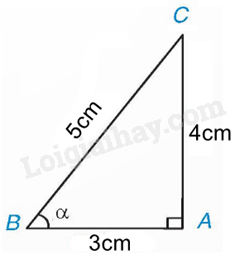
Theo định nghĩa của tỉ số lượng giác, ta có:

\(\sin \alpha  = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha  = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha  = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha  = \frac{{AB}}{{AC}} = \frac{3}{4}\)

2. Tỉ số lượng giác của một số góc đặc biệt

Bảng giá trị lượng giác của các góc \({30^0},{45^0},{60^0}\)

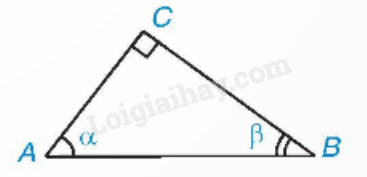
3. Tỉ số lượng giác của hai góc phụ nhau

Định lí về tỉ số lượng giác của hai góc phụ nhau

Cho \(\alpha \) và \(\beta \) là hai góc phụ nhau, ta có:

\(\sin \alpha  = \cos \beta \), \(\cos \alpha  = \sin \beta \), \(\tan \alpha  = \cot \beta \), \(\cot \alpha  = \tan \beta \).

Ví dụ:

\(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30' = \sin \left( {{{90}^0} - {{52}^0}30'} \right) = \sin {37^0}30';\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\)

4. Tính các tỉ số lượng giác của một góc khi biết số đo góc và tính số đo góc khi biết tỉ số lượng giác bằng máy tính cầm tay.

a) Tính tỉ số lượng giác khi biết số đo góc

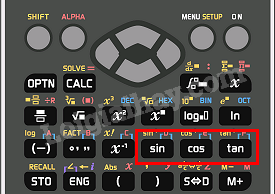
Ngoài đơn vị độ, người ta còn dùng đơn vị phút (‘) và giây (“) để đo góc chính xác hơn với \({1^0} = 60';1' = 60''\).

Để tính các tỉ số lượng giác sin, côsin và tang của một góc, ta sử dụng các phím

Để tính giá trị côtang của một góc \(\alpha \), ta tính tang của \({90^0} - \alpha \) hoặc tính giá trị \(\frac{1}{{\tan \alpha }}\).

b) Tìm số đo góc khi biết tỉ số lượng giác

Khi biết tỉ số lượng giác của một góc nhọn, ta cũng có thể sử dụng máy tính cầm tay để tính số đo của góc nhọn đó. Để tìm góc nhọn \(\alpha \), ta bấm:

Một số công thức mở rộng:

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)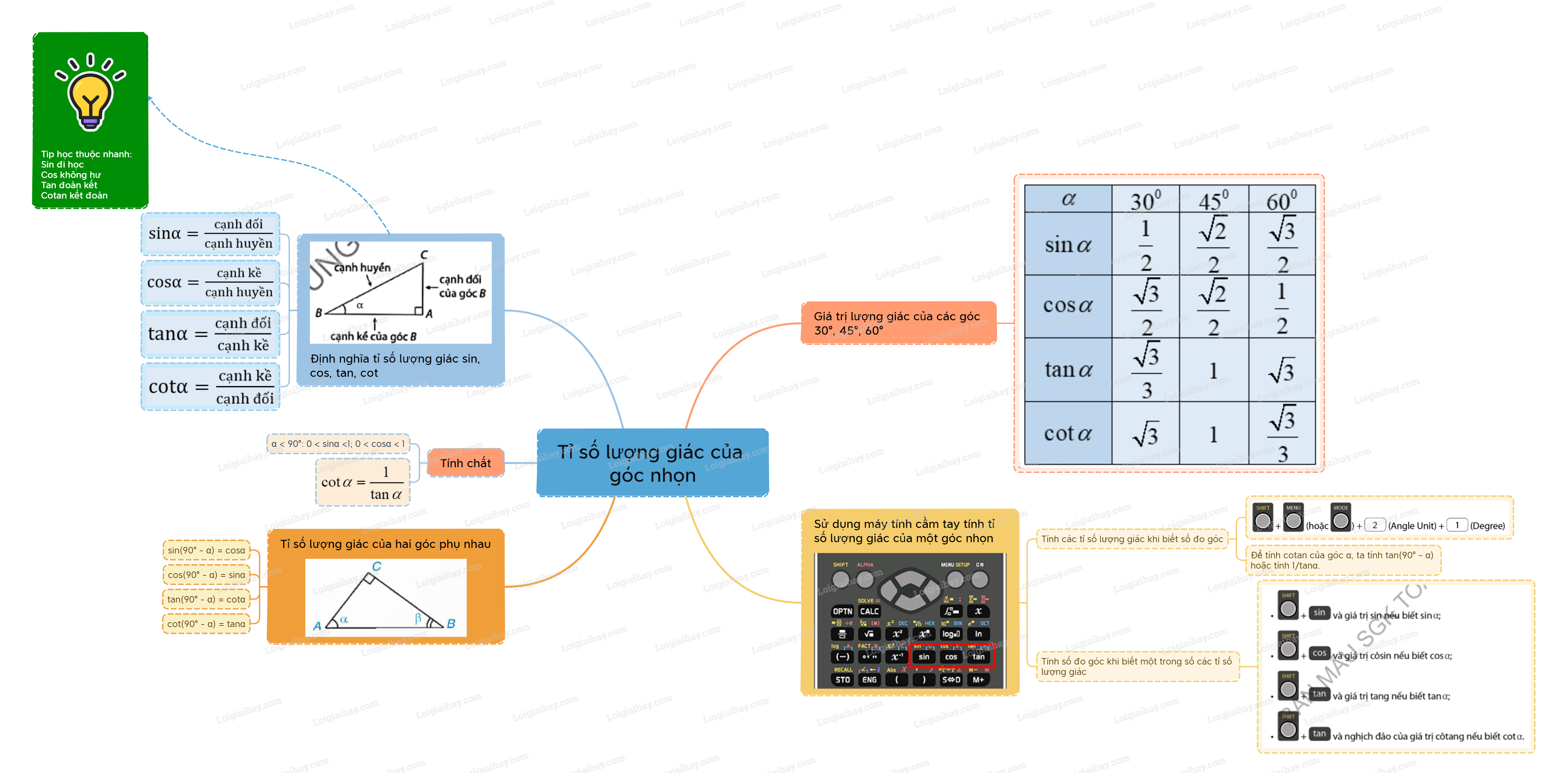