Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Cùng khám phá1. Mở đầu về bất phương trình Định nghĩa bất phương trình Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) thì ta nói cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) là một bất phương trình ẩn x. A(x) và B(x) lần lượt được gọi là vế trái và vế phải của bất phương trình. 1. Mở đầu về bất phương trình Định nghĩa bất phương trình
Nghiệm của bất phương trình
Ví dụ: Số -2 là nghiệm của bất phương trình 2x−10<0 vì 2.(−2)−10=−4−10=−14<0. Số 6 không là nghiệm của bất phương trình 2x−10<0 vì 2.6−10=12−10=2>0. 2. Bất phương trình bậc nhất một ẩn Định nghĩa
Ví dụ: 3x+16≤0; −3x>0 là các bất phương trình bậc nhất một ẩn x. x2−4≥0 không phải là một bất phương trình bậc nhất một ẩn x vì x2−4 là một đa thức bậc hai. 3x−2y<2 không phải là một bất phương trình bậc nhất một ẩn vì đa thức 3x−2y là đa thức với hai biến x và y. 3. Cách giải bất phương trình bậc nhất một ẩn Giải một bất phương trình nghĩa là tìm tất cả các nghiệm của nó.
Ví dụ: Giải bất phương trình −2x−4>0 Lời giải: Ta có: −2x−4>0−2x>0+4−2x>4x<4.(−12)x<−2 Vậy nghiệm của bất phương trình là x<−2. Lưu ý: Ở Bước 1, ta đã thực hiện quy tắc sau, gọi là quy tắc chuyển vế: Khi chuyển một hạng tử từ vế này sang vế kia, ta phải đổi dấu hạng tử đó. Quy tắc thực hiện ở Bước 2 gọi là quy tắc nhân với một số: Khi nhân hai vế của một bất phương trình cùng một số khác 0, ta phải: - Giữ nguyên chiều bất phương trình nếu số đó dương; - Đổi chiều bất phương trình nếu số đó âm. Nhờ hai quy tắc này, ta có thể giải được nhiều bất phương trình phức tạp hơn. 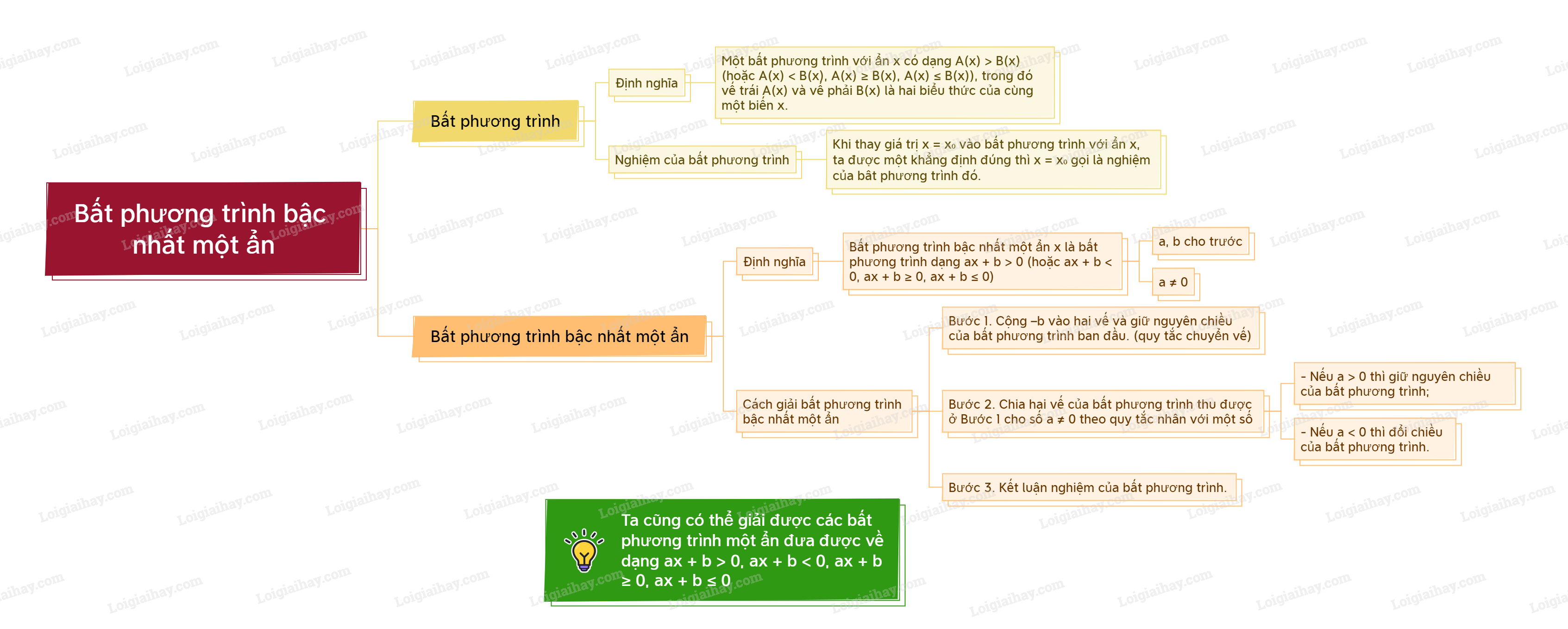
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|



















