Bài ôn tập cuối chương I trang 14, 15, 16 SBT Vật lí 11 Kết nối tri thức với cuộc sống

I.1

Một vật đang thực hiện một dao động điều hoà dưới tác dụng của một lực đàn hồi. Chọn câu đúng:

A. Khi vật đi qua vị trí cân bằng thì gia tốc đạt giá trị cực đại.

B. Khi vật ở vị trí biên thì lực đổi chiều.

C. Khi vật đi từ vị trí cân bằng đền vị trí biên thì gia tốc ngược chiều với vận tốc.

D. Khi vật đi từ vị trí biên đến vị trí cân bằng thì độ lớn của gia tốc tăng dần.

Phương pháp giải:

Phương trình của gia tốc có dạng :  \(a = A{\omega ^2}\cos \left( {\omega t + \varphi  + \pi } \right)\)

• Khi vật ở VTCB : \(a = 0\)
• Khi vật ở vị trí biên : \(a =  \pm {\omega ^2}A\)

Gia tốc luôn hướng về vị trí cân bằng

Trong giao động điều hòa vật đổi chiều khi vật ở vị trí biên

Lời giải chi tiết:

Ta có gia tốc luôn hướng về vị trí cân bằng và khi vật đi từ VTCB đến vị trí biên thì gia tốc ngược chiều với vận tốc

Đáp án : C

I.2

Một vật đang thực hiện một dao động điều hoà quanh vị trí cân bằng O. Hai vị trí biên là M và N (Hình ...). Trong giai đoạn nào sau đây của chuyển động thì vận tốc và gia tốc cùng chiều nhau?

A. Từ O đến M.

B. Từ N đến O.

C. Từ O đến N.

D.Từ M đến N.             

Phương pháp giải:

Gia tốc luôn hướng về vị trí cân bằng

Lời giải chi tiết:

Gia tốc luôn hướng về VTCB nên khi vật đi từ N về O thì vận tốc và gia tốc cùng chiều nhau .

Đáp án : B

I.3

Tìm phát biểu sai về gia tốc của một vật dao động điều hoà:

A. Gia tốc đổi chiều khi vật đi qua vị trí cân bằng.

B. Gia tốc luôn ngược chiều với vận tốc.

C. Gia tốc luôn hướng về vị trí cân bằng.

D. Gia tốc biến đổi ngược pha với li độ.

Phương pháp giải:

Phương trình của gia tốc có dạng :  \(a = A{\omega ^2}\cos \left( {\omega t + \varphi  + \pi } \right)\)

• Khi vật ở VTCB : \(a = 0\)
• Khi vật ở vị trí biên : \(a =  \pm {\omega ^2}A\)

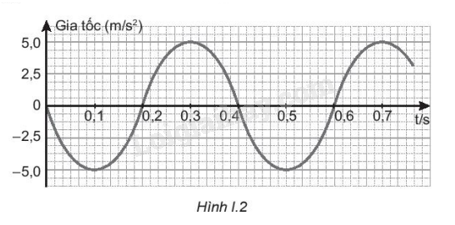
Gia tốc luôn hướng về vị trí cân bằng

Lời giải chi tiết:

Gia tốc luôn hướng về VTCB nên khi vật đi từ biên về VTCB thì vận tốc và gia tốc cùng chiều nhau

Đáp án : B

I.4

Một con lắc lò xo gồm một lò xo có độ cứng không đổi . Khi khối lượng quả nặng là m thì tần số dao động là 1 Hz. Khi khối lượng quả nặng là 2m thì tần số là :

A. 2 Hz

B. \(\sqrt 2 \)Hz

C. \(\frac{1}{{\sqrt 2 }}\)Hz

D. 0,5 Hz

Phương pháp giải:

Chu kì của con lắc lò xo : \(T = 2\pi \sqrt {\frac{m}{k}} \)

Tần số của con lắc lò xo : \(f = \frac{1}{T}\)

Lời giải chi tiết:

Ta có \(\frac{{{f_1}}}{{{f_2}}} = \sqrt {\frac{k}{{{m_1}}}} .\sqrt {\frac{{{m_2}}}{k}}  = \sqrt {\frac{{{m_2}}}{{{m_1}}}}  = \sqrt {\frac{{2m}}{m}}  = \sqrt 2 Hz =  > {f_2} = \frac{{{f_1}}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }}Hz\)

Đáp án : C

I.5

Một con lắc lò xo nằm ngang, đang thực hiện dao động điều hoà. Tìm phát biểu sai:

A. Động năng của vật nặng và thế năng đàn hồi của lò xo là hai thành phần tạo thành cơ năng của con lắc

B. Động năng và thế năng biến thiên tuần hoàn với cùng một tần số như nhau.

C. Khi vật ở một trong hai vị trí biên thì thế năng đạt giá trị cực đại.

D. Động năng và thế năng biến thiên tuần hoàn với cùng chu kì như chu kì của dao động.

Phương pháp giải:

Động năng và thế năng biến thiên tuần hoàn cùng tần số : \({f_d} = {f_t} = 2{f_0}\)

Cơ năng của vật dao động : \(W = {W_d} + {W_t} = \frac{1}{2}m{\omega ^2}{A^2}\)

Thế năng của vật : \(\)\({W_t} = \frac{1}{2}m{\omega ^2}{x^2}\)

Lời giải chi tiết:

Động năng và thế năng biến thiên tuần hoàn với chu kì bằng 2 chu kì của dao động

Đáp án : D

I.6

Tìm phát biểu sai về dao động tắt dần của con lắc lò xo :

A. Cơ năng của vật luôn giảm dần.

B. Động năng của vật có lúc tăng, lúc giảm.

C. Động năng của vật luôn giảm dần.

D. Thế năng có lúc tăng lúc giảm

Phương pháp giải:

Dao động tắt dần là dao động có biên độ , cơ năng giảm dần theo thời gian

Lời giải chi tiết:

Trong dao động tắt dần, động năng và thế năng của vật có lúc tăng, lúc giảm => Động năng của vật luôn giảm dần là sai

Đáp án : C

I.7

Ích lợi của hiện tượng cộng hưởng được ứng dụng trong trường hợp nào sau đây?

A. Chế tạo máy phát tần số

B. Chế tạo bộ phận giảm xóc của ô tô, xe máy.

C. Lắp đặt các động cơ điện trong nhà xưởng.

D. Thiết kế các công trình ở những vùng thường có địa chấn

Phương pháp giải:

Sử dụng lí thuyết ứng dụng của hiện tượng cộng hưởng

Lời giải chi tiết:

Ích lợi của hiện tượng cộng hưởng được ứng dụng trong : Chế tạo máy phát tần số

Đáp án : A

I.8

Một vật dao động điều hoà với chu kì T, nếu vào thời điểm ban đầu, vật đi qua vị trí cân bằng thì vào thời điểm \(\frac{T}{{12}}\), tỉ số giữa động năng và thế năng của vật.

Phương pháp giải:

Cơ năng của vật dao động : \(W = {W_d} + {W_t} = \frac{1}{2}m{\omega ^2}{A^2}\)

Thế năng của vật : \(\)\({W_t} = \frac{1}{2}m{\omega ^2}{x^2}\)

động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\).

Lời giải chi tiết:

Gia sử pha ban đầu của vật là \(\frac{\pi }{2}\)

Sau khoảng thời gian \(t = \frac{T}{{12}}\) thì vật quay được góp \(\Delta \varphi  = \frac{\pi }{6}\)=> Thời điểm \(t = \frac{T}{{12}}\)

vật ở vị trí góc \(\frac{{2\pi }}{3}\)trên đường tròn lượng giác \( =  > x = \frac{{ - A}}{2}\)

=>\({W_t} = \frac{1}{4}W =  > {W_d} = \frac{3}{4}W =  > \frac{{{W_d}}}{{{W_t}}} = 3\)

I.9

Một vật dao động điều hoà dọc theo trục Ox nằm ngang , gốc O và mốc thế năng ở vị trí cân bằng. Cứ sau 0,5 s thì động năng lại bằng thế năng và trong thời gian 0,5 s vật đi được đoạn đường dài nhất bằng \(4\sqrt 2 \) cm. Chọn t= 0 là lúc vật qua vị trí cân bằng theo chiều dương. Viết phương trình dao động của vật.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:

+ \(x\) là li độ dao động.

+ \(A\) là biên độ dao động.

+ \(\omega \) là tần số góc của dao động.

+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.

+\(\varphi \) là pha ban đầu.

Lời giải chi tiết:

Cứ sau 0,5 s thì động năng lại bằng thế năng => \(t = \frac{T}{4} =  > T = 2s =  > \omega  = \pi rad/s\)

Quãng đường lớn nhất vật đi được trong \(\frac{1}{4}\)chu kì là : \(S = A\sqrt 2  =  > A = 4cm\)

Chọn t=0 lúc vật đi qua VTCB theo chiều dương => Pha ban đầu của vật là : \(\varphi  =  - \frac{\pi }{2}\)

=>Phương trình dao động của vật là : \(x = 4\cos \left( {\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\)

I.10

Một con lắc lò xo gồm lò xo có độ cứng k = 160 N/m và vật nặng có khối lượng m = 400 g, đặt trên mặt phẳng nằm ngang. Hệ số ma sát trượt giữa vật và mặt phẳng nằm ngang là \(\mu  = 0,0005\). Lấy \(g = 10m/{s^2}\). Kéo vật lệch khỏi vị trí cân bằng một đoạn 5 cm (theo phương của trục lò xo). Tại t= 0, buông nhẹ để vật dao động, xem rằng tần số dao động không đổi .Tính thời gian kể từ lúc vật bắt đầu dao động cho đến khi vật dừng hẳn.

Phương pháp giải:

Cơ năng của con lắc lò xo : \(W = \frac{1}{2}k{A^2}\)

Độ biến thiên cơ năng : \(\Delta W = {A_{ms}}\)

Công của lực ma sát : \({A_{ms}} = {F_{ms}}.s.\cos \alpha \)

Thời gian giữa hai lần vật đi qua vị trí biên liên tiếp là : \(\frac{T}{2}\)

Lời giải chi tiết:

Chu kì của con lắc : \(T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{0,4}}{{160}}}  = 0,1\pi (s)\)

Giả sử ban đầu vật ở biên dương có li độ \({A_0}\), sau khi qua VTCB vật đến biên âm có li độ A . Quãng đường vật đi được là : \(S = {A_0} + A\)

Công của lực ma sát khi vật đi được quãng đườn S là :

\({A_{ms}} = {F_{ms}}.S.\cos {180^o} =  - \mu mg({A_0} + A)\)

Độ biến thiên cơ năng của con lắc là :

\(\Delta W = W - {W_0} = {A_{ms}} =  > \frac{1}{2}k{A^2} - \frac{1}{2}kA_0^2 =  - \mu mg\left( {{A_0} + A} \right)\)

\( =  > \Delta A = {A_0} - A = \frac{{2\mu mg}}{k} =  > \Delta A = \frac{{2.0,0005.0,4.10}}{{160}} = 2,{5.10^{ - 5}}(m)\)

Số nửa chu kì vật thực hiện được cho đến khi dừng hẳn là :

\(N = \frac{A}{{\Delta A}} = \frac{{0,05}}{{2,{{5.10}^{ - 5}}}} = 2000\)

Thời gian kể từ lúc vật bắt đầu dao động cho đến khi vật dừng hẳn là :

\(t = N.\frac{T}{2} = 2000.\frac{{0,1\pi }}{2} \approx 314(s)\)

I.11

Hình I.2 mô tả sự biến thiên gia tốc theo thời gian của một vật dao động điều hoà.

a) Viết phương trình gia tốc theo thời gian.

b) Viết phương trình li độ và vận tốc theo thời gian

Phương pháp giải:

Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:

+ \(x\) là li độ dao động.

+ \(A\) là biên độ dao động.

+ \(\omega \) là tần số góc của dao động.

+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.

+\(\varphi \) là pha ban đầu.

Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi  + \frac{\pi }{2}} \right)\)

• Khi vật ở VTCB : \(v =  \pm \omega A\)
• Khi vật ở vị trí biên : \(v = 0\)

Phương trình của gia tốc có dạng :  \(a = A{\omega ^2}\cos \left( {\omega t + \varphi  + \pi } \right)\)

• Khi vật ở VTCB : \(a = 0\)
• Khi vật ở vị trí biên : \(a =  \pm {\omega ^2}A\)

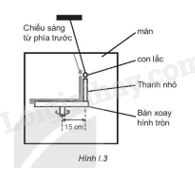
Lời giải chi tiết:

a) Dựa vào đồ thì ta có :

Tại t = 0 , \(a =  - {\omega ^2}x = 0 =  > x = 0\)=> Vật ở VTCB và vật chuyển động theo chiều dương => \({\varphi _0} =  - \frac{\pi }{2}\)

Chu kì dao động \(T = 0,4s =  > \omega  = 5\pi (rad/s)\)

=> Phương trình của gia tốc : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi  + \pi } \right) = 5\cos \left( {5\pi t + \frac{\pi }{2}} \right)\)

b) Dựa vào đồ thị ta có :

Gia tốc cực đại : \(a = {\omega ^2}A = 5 =  > A = \frac{5}{{{\omega ^2}}} = \frac{5}{{25{\pi ^2}}} = \frac{1}{{5{\pi ^2}}}(m) = 0,02m = 2cm\)

=> Phương trình dao động của vật : \(x = A\cos \left( {\omega t + \varphi } \right) = 2\cos \left( {5\pi t - \frac{\pi }{2}} \right)(cm)\)

=> Phương trình của vận tốc của vật  : \(v = A\omega \cos \left( {\omega t + \varphi  + \frac{\pi }{2}} \right) = 10\pi \cos \left( {5\pi t} \right)\left( {cm/s} \right)\)

I.12

Hình I.3 là sơ đồ của một bàn xoay hình tròn, có gắn một thanh nhỏ cách tâm bàn 15 cm. Bàn xoay được chiều sáng từ bên cạnh phía trước màn để bóng đổ lên màn hình. Một con lắc đơn được đặt sau bàn xoay và làm cho dao động điều hoà với biên độ bằng khoảng cách từ thanh nhỏ đền tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là \(2\pi \) rad/s và bóng của thanh nhỏ luôn trùng với bóng của con lắc trên màn hình.

a) Tại sao nói dao động của bóng của thanh nhỏ và quả lắc là đồng pha ?

b) Viết phương trình mô tả li độ x của con lắc khỏi vị trí cân. Chọn gốc thời gian là lúc con lắc ở vị trí hiển  thị trong sơ đồ.

c) Bàn xoay đi một góc \({60^0}\) từ vị trí ban đầu. Tính li độ của con lắc và tốc độ của nó tại thời điểm này. Bàn xoay phải quay thêm một góc nào nữa trước khi nó có tốc độ này trở lại?

Phương pháp giải:

Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:

+ \(x\) là li độ dao động.

+ \(A\) là biên độ dao động.

+ \(\omega \) là tần số góc của dao động.

+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.

+\(\varphi \) là pha ban đầu.

Lời giải chi tiết:

a)    Dao động của bóng của thanh nhỏ và quả nặng đồng pha với nhau vì chúng luôn xuất hiện cùng lúc .

b)    Biên độ dao động của con lắc A= 15 cm

Tần số góc \(\omega  = 2\pi (rad/s)\). Từ hình vẽ và hướng di chuyển của con lắc ta có pha ban đầu \(\varphi  = 0\)

Phương trình dao động của con lắc là : \(x = 15\cos 2\pi t\left( {cm} \right)\)

c)    Bàn xoay đi một góc \({60^o}\)từ vị trí ban đầu ta có pha dao động của con lắc là \(\frac{\pi }{3}\)

Li độ của con lắc là \(x = 7,5cm\)

Vận tốc của con lắc là \(v = \left| { \pm \omega \sqrt {{A^2} - {x^2}} } \right| = 15\sqrt 3 \pi (cm/s)\)