Bài 1. Dao động điều hòa trang 4, 5 SBT Vật lí 11 Kết nối tri thức với cuộc sốngMột chất điểm dao động điều hoà có quỹ đạo là một đoạn thằng dài 10 cm. Biên độ dao động của chất điểm là:
Lựa chọn câu để xem lời giải nhanh hơn
1.1 Một chất điểm dao động điều hoà có quỹ đạo là một đoạn thằng dài 10 cm. Biên độ dao động của chất điểm là: A. 5 cm. B. -5cm. C. 10 cm. D. -10cm. Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\) Vật dao động từ vị trí biên âm về biên dương .Nên chiều dài quỹ đạo \(L = 2A\) Lời giải chi tiết: Ta có chiều dài quỹ \(L = 2A = 10 = > A = 5\left( {cm} \right)\) Đáp án A 1.2 Một chất điểm dao động điều hoà trong 10 dao động toàn phần đi được quãng đường dài 120 cm. Quỹ đạo của dao động có chiều dài là A. 6 cm. B. 12 cm. C. 3 cm. D. 9 cm. Phương pháp giải: Vận dụng kiến thức
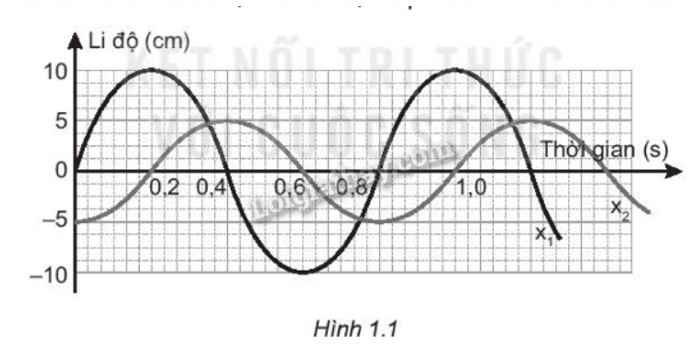
Lời giải chi tiết: Ta có : Quãng đường trong một dao động toàn phần \(S = 4A\) 10 dao động toàn phần đi được \(S' = 40A = 120\left( {cm} \right)\) => Biên độ dao động\(A = 3\left( {cm} \right)\) Chiều dài quỹ đạo \(L = 2A = 6\left( {cm} \right)\) Đáp án : A 1.3 Một chất điểm dao động điều hoà với phương trình : \(x = 5\cos \left( {10\pi + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\). Li độ của vật khi pha dao động bằng \(\left( \pi \right)\) là A. 5 cm. B. -5cm. C. 2,5 cm. D. -2.5 cm. Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: Thay pha dao động bằng \(\left( \pi \right)\)vào phương trình \(x = 5\cos \left( {10\pi + \frac{\pi }{3}} \right)\)ta có : x= 5cos\(\left( \pi \right)\)\( = - 5\left( {cm} \right)\) Đáp án : B 1.4 Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 5\sqrt 3 \cos \)\(x = 5\sqrt 3 \cos \left( {10\pi + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\) .Tại thời điểm \(t = 1\left( s \right)\) thì li độ của vật bằng: A. 25cm. B. \( - 5\sqrt 3 \) cm. C. 5 cm, D. \(2,5\sqrt 3 \)cm. Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: Thay t= 1 s vào phương trình dao động ta có : \(x = 5\sqrt 3 \cos \left( {10\pi + \frac{\pi }{3}} \right) = 2,5\sqrt 3 \left( {cm} \right)\) Đáp án : D 1.5 Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 6\cos \left( {10\pi t + \frac{\pi }{3}} \right)\)\(\left( {cm} \right)\).Li độ của vật khi pha dao động bằng \(\left( { - \frac{\pi }{3}} \right)\) là: A. 3 cm B. -3 cm C. 4.24 cm D. -4.24 cm Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: Thay pha dao động bằng \(\left( { - \frac{\pi }{3}} \right)\)vào phương trình dao động ta có : \(x = 6\cos \left( { - \frac{\pi }{3}} \right)\)\( = 3\left( {cm} \right)\) Đáp án : A 1.6 Một chất điểm M chuyền động đều trên một đường tròn, bán kính R, vận tốc góc . Hình chiều của M trên đường kính là một dao động điều hoà có A. biên độ R B. biên độ 2R. C. pha ban đầu t D. quỹ đạo 4R Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\) Lời giải chi tiết: Điểm M thuộc đường trong bán kính R , điểm Q là hình chiếu của M trên đường kính chuyển động qua lại quanh VTCB => biên độ dao động của Q là OA = OM = R Đáp án A 1.7 Phương trình dao động của một vật có dạng:\(x = - A\cos \left( {\omega t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Pha ban đầu của dao động là A. \(\frac{\pi }{3}\) cm B. \( - \frac{\pi }{3}\) cm C. \(\frac{{2\pi }}{3}\) cm D. \( - \frac{{2\pi }}{3}\) cm Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: Phương trình dao động điều hoà \(x = - A\cos \left( {\omega t + \frac{\pi }{3}} \right)\)\( = A\cos \left( {\omega t + \frac{\pi }{3} - \pi } \right) = A\cos \left( {\omega t - \frac{{2\pi }}{3}} \right)\) Pha ban đầu của dao động là : \(\varphi = - \frac{{2\pi }}{3}\) Đáp án : D 1.8 Phương trình dao động điều hoà là \(x = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\). Hãy cho biết biên độ, pha ban đầu và pha ở thời điểm t của dao động. Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: Từ phương trình \(x = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)\) ta có : => Biên độ dao động : \(A = 5\left( {cm} \right)\) => Pha ban đầu của dao động :\(\varphi = \frac{\pi }{3}\) => Pha của dao động ở thời điểm t : \(\left( {\omega t + \varphi } \right) = 2\pi t + \frac{\pi }{3}\) 1.9 Một chất điểm dao động điều hoà có phương trình li độ theo thời gian là: \(x = 10\cos \left( {\frac{\pi }{3}t + \frac{\pi }{2}} \right)\left( {cm} \right)\) a) Tính quãng đường vật đi được sau 2 dao động. b) Tính li độ của vật khi \(t = 6\left( s \right)\). Phương pháp giải: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Quãng đường trong một dao động toàn phần \(S = 4A\) Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với: + \(x\) là li độ dao động. + \(A\) là biên độ dao động. + \(\omega \) là tần số góc của dao động. + \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t. +\(\varphi \) là pha ban đầu. Lời giải chi tiết: a) Quãng đường vật đi được sau 2 dao động \(S = 8A = 8.10 = 80\left( {cm} \right)\) b) Thay \(t = 6\left( s \right)\) vào phương trình dao động ta được: \(x = 10\cos \left( {\frac{\pi }{3}.6 + \frac{\pi }{2}} \right) = 0\)\(\) 1.10 Đồ thị li độ theo thời gian x1, x2, của hai chát điểm dao động điều hoà được mô tả như Hình 1.1. Xác định biên độ và pha ban đầu của mỗi dao động. Phương pháp giải:
Lời giải chi tiết: Từ đồ thị ta thấy: Xét \({x_1}\) - Biên độ dao động là giá trị lớn nhất của li độ:\(A = x\max = 10\left( {cm} \right)\) - Lúc t=0, con lắc đang ở VTCB : \(x = 0\) và \(v > 0\) => \(x = A\cos \varphi \) <=> \(\cos \varphi = 0 = > \varphi = - \frac{\pi }{2}\) Vậy dao động \({x_1}\)có :
Xét \({x_2}\) - Biên độ dao động là giá trị lớn nhất của li độ: \(A = x\max = 5\left( {cm} \right)\) - Lúc t=0, con lắc đang ở biên âm \(x = - A = - 5\left( {cm} \right)\) và \(v > 0\) => \(x = A\cos \varphi \)<=> \(\cos \varphi = - 1 = > \varphi = \pi \) Vậy dao động \({x_2}\)có :
 Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
