Bài 5. Động năng. Thế năng. Sự chuyển hóa năng lượng trong dao động điều hòa trang 9, 10, 11, 12 SBT Vật lí 11 Kết nối tri thức với cuộc sốngĐại lượng nào sau đây tăng gấp đôi khi tăng gấp đôi biên độ của dao động điều hoà của con lắc lò xo? Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
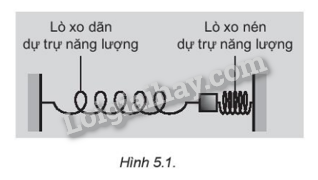
5.1 Đại lượng nào sau đây tăng gấp đôi khi tăng gấp đôi biên độ của dao động điều hoà của con lắc lò xo? A. Cơ năng của con lắc. B. Động năng của con lắc. C. Vận tốc cực đại. D. Thế năng của con lắc. Phương pháp giải: Vận dụng kiến thức về các đại lượng đặc trưng của dao động điều hòa và kiến thức về động năng , thế năng , cơ năng. Lời giải chi tiết: Ta có \({v_{_{\max }}} = A\omega \) vậy khi tăng gấp đôi A thì vận tốc cực đại tăng gấp đôi . Đáp án : C 5.2 Cơ năng của một chất điểm dao động điều hoà tỉ lệ thuận với A. chu kì dao động. B. biên độ dao động. C. bình phương biên độ dao động. D. bình phương chu kì dao động. Phương pháp giải: Vận dụng kiến thức về cơ năng : trong dao động điều hòa, có sự chuyển hóa qua qua lại giữa động năng và thế năng của vật, còn cơ năng, tức tổng động năng và thế năng thì được bảo toàn . Lời giải chi tiết: Ta có \(W = {W_d} + {W_t} = \frac{1}{2}m{\omega ^2}{A^2}\) => Cơ năng của một chất điểm dao động điều hoà tỉ lệ thuận với bình phương biên độ dao động Đáp án : C 5.3 Trong dao động điều hoà thì tập hợp 3 đại lượng nào sau đây không thay đồi theo thời gian? A. Lực kéo về ; vận tốc ; năng lượng toàn phần. B. Biên độ ; tần số góc ; gia tốc. C. Động năng ; tần số ; lực kéo về. D. Biên độ , tần số góc ; năng lượng toàn phần. Phương pháp giải: Vận dụng kiến thức về dao động điều hòa . Vận dụng kiến thức về các đại lượng đặc trưng của dao động điều hòa và kiến thức về động năng , thế năng , cơ năng. Lời giải chi tiết: Trong dao động điều hòa thì biên độ, tần số và năng lượng toàn phần không thay đổi theo thời gian. Đáp án : D 5.4 Phương trình dao động của một chất điểm dao động điều hoà là: \(x = A\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)(cm)\) Động năng của nó biến thiên theo thời gian theo A. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 + \cos \left( {2\omega t + \frac{\pi }{3}} \right)} \right]\) B. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 - \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\) C. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{2}\left[ {1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\) D. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\) Phương pháp giải: Vận dụng kiến thức về động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Lời giải chi tiết: Ta có \(x = A\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)\) => \(v = - A\omega \sin \left( {\omega t + \frac{{2\pi }}{3}} \right)\) \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{A^2}{\omega ^2}\left( {1 - {{\cos }^2}\left( {\omega t + \frac{{2\pi }}{3}} \right)} \right) = \frac{1}{2}m{A^2}{\omega ^2}\left( {1 - \frac{{1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)}}{2}} \right)\) \( = \frac{1}{2}m{A^2}{\omega ^2}\left( {\frac{{1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)}}{2}} \right)\)\( = \frac{1}{4}m{A^2}{\omega ^2}\left( {1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right)\) Đáp án : D 5.5 Một chất điểm dao động điều hoà. Biết khoảng thời gian giữa năm lần liên tiếp động năng của chất điểm bằng thế năng của hệ là 0,4 s. Tần số của dao động là A. 2,5 Hz. B. 3,125 Hz. C. 5 Hz. D. 6,25 Hz. Phương pháp giải: Vận dụng kiến thức về động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Và thế năng của vật : \(\)\({W_t} = \frac{1}{2}m{\omega ^2}{x^2}\) Lời giải chi tiết: Vị trí động năng bằng thế năng \({W_d} = {W_t} = > \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{\omega ^2}{x^2} = > {A^2} - {x^2} = {x^2} = > 2{x^2} = {A^2} = > x = \frac{{A\sqrt 2 }}{2}\) => Khoảng thời gian giữa năm lần liên tiếp động năng của chất điểm bằng thế năng của hệ là 0,4 s => \(\frac{{4T}}{4} = 0,4 = > T = 0,4 = > f = \frac{1}{T} = 2,5(Hz)\) Đáp án : A 5.6 Một chất điểm có khối lượng m, dao động điều hoà với biên độ A, tần số góc \(\omega \). Động năng cực đại của chất điểm là A. \(\frac{{m.{A^2}.{\omega ^2}}}{2}\) B. \(\frac{{{A^2}.{\omega ^2}}}{{2m}}\) C. \(\frac{{m.A.{\omega ^2}}}{2}\) D. \(\frac{{m.{A^2}.\omega }}{2}\) Phương pháp giải: Vận dụng kiến thức về động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Khi vật đi từ VTCB tới vị trí biên thì động năng của vật đang từ cực đại giảm đến 0. Khi vật đi từ vị trí biên về VTCB thì động năng của vật tăng từ 0 đến giá trị cực đại. Lời giải chi tiết: Ta có \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right)\) . Khi vật đi từ vị trí biên về VTCB thì động năng của vật tăng từ 0 đến giá trị cực đại. => x = 0 \( = > {W_d}\max = \frac{1}{2}m{\omega ^2}{A^2}\) Đáp án : A 5.7 Một vật có khối lượng m = 1 kg, dao động điều hoà với chu kì \(T = 0,2\pi \left( s \right)\), biên độ dao động bằng 2 cm. Tính cơ năng của dao động. Phương pháp giải: Vận dụng kiến thức về cơ năng. Trong dao động điều hòa, có sự chuyển hóa qua qua lại giữa động năng và thế năng của vật, còn cơ năng, tức tổng động năng và thế năng thì được bảo toàn : \(W = {W_d} + {W_t} = \frac{1}{2}m{\omega ^2}{A^2}\) Lời giải chi tiết: Đổi 2cm = 0,02 m Ta có \(T = 0,2\pi = > \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,2\pi }} = 10(rad/s)\) => Cơ năng của vật : \(W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}{.1.10^2}.0,{02^2} = 0,02(J)\) 5.8 Một chất điểm có khối lượng 100 g dao động điều hoà trên quỹ đạo là đoạn thẳng MN (dài hơn 8 cm). Tại điểm P cách M 4 cm và tại điểm Q cách N 2 cm chất điểm có động năng tương ứng là \({32.10^{ - 3}}\) J và \({18.10^{ - 3}}\)J. Tính tốc độ trung bình khi vật đi từ M đến N. Phương pháp giải: Vận dụng kiến thức về động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Lời giải chi tiết: Đổi 100g = 0,1 kg ; 4cm = 0,04 m ; 2cm = 0,02 m Ta có Động năng của vật tại vị trí P \({W_d}p = \frac{1}{2}m{v^2}_p = {32.10^{ - 3}}J = > {v_P} = \sqrt {\frac{{{{2.32.10}^{ - 3}}}}{{0,1}}} = 0,8m/s\) Động năng của vật tại vị trí Q \({W_d}Q = \frac{1}{2}m{v^2}_Q = {18.10^{ - 3}}J = > {v_Q} = \sqrt {\frac{{{{2.18.10}^{ - 3}}}}{{0,1}}} = 0,6m/s\) \( = > \frac{{{v_p}}}{{{v_Q}}} = \sqrt {\frac{{{A^2} - {x_p}^2}}{{{A^2} - {x_Q}^2}}} = \frac{{A - 2}}{{A - 1}} = \frac{8}{9} = > A = 10(cm)\) Ta có : \({v_p} = \omega \sqrt {{A^2} - {{(A - 4)}^2}} = 0,8 = > \omega = \frac{{0,8}}{{\sqrt {0,1 - 0,36} }} = 10(rad/s)\) Ta có Vận tốc trung bình khi vật đi từ M đến N \({v_{tb}} = \frac{S}{t} = \frac{{MN}}{{\frac{T}{2}}} = \frac{{2A}}{T} = \frac{{2A.\omega }}{{2\pi }} = \frac{{A\omega }}{\pi } = \frac{{10.10}}{\pi } = \frac{{100}}{\pi }(m/s)\) 5.9 Một con lắc lò xo treo thẳng đứng vào điểm I có định, quả cầu có khối lượng 100 g. Con lắc dao động điều hoà theo phương trình: \(x = 4\cos 10\sqrt 5 t(cm)\)với t tính theo giây. Lấy g = 10 \(m/{s^2}\). Tính lực đàn hồi cực đại và cực tiều do lò xo tác dụng lên điểm I. Phương pháp giải: Tần số góc của con lắc lò xo : \(\)\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} \) Lực đàn hồi của lò xo : \({F_{dh}} = k\Delta l\) Lời giải chi tiết: Tần số góc của con lắc lò xo là : \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta l}}} = > 10\sqrt 5 = \sqrt {\frac{k}{{0,1}}} = \sqrt {\frac{{10}}{{\Delta l}}} \) \( = > \{ _{\Delta l = 0,02(m)}^{k = 50(N/m)}\) Biên độ dao động của con lắc : \(A = 4cm > \Delta l\) => Vật có thể giãn có thể nén trong quá trình dao động => Lực đàn hồi dãn max khi vật ở vị trí thấp nhất : \({F_{dh\max }} = k.(\Delta l + A) = 50.(0,02 + 0,04) = 3(N)\) => Lực đàn hồi nén max khi vật ở vị trí cao nhất : \({F_{dh\max }} = k.(A - \Delta l) = 50.(0,04 - 0,02) = 1(N)\) => Lực đàn hồi min khi vật ở vị trí cân bằng => \({F_{dh\min }} = 0\) 5.10 Một con lắc lò xo treo thẳng đứng. Biết rằng trong quá trình dao động tỉ số giữa lực đàn hồi cực đại và cực tiểu là \(\frac{7}{3}\) , biên độ dao động là 10 cm. Lấy g = 10 \(m/{s^2}\) . Tính tần số dao động của vật. Phương pháp giải: Chu kì dao động của lò xo : \(T = 2\pi \sqrt {\frac{{\Delta l}}{g}} \) Lực đàn hồi của lò xo : \({F_{dh}} = k\Delta l\) Lời giải chi tiết: Ta có \(\frac{{{F_{dh\max }}}}{{{F_{dh\min }}}} = \frac{{k.(A + \Delta l)}}{{k.(A - \Delta l)}} = > \frac{{\Delta l + 10}}{{\Delta l - 10}} = \frac{7}{3} = > \Delta l = 25(cm)\) \( = > T = 2\pi \sqrt {\frac{{\Delta l}}{g}} = 2\pi \sqrt {\frac{{0,25}}{{10}}} = \frac{\pi }{{\sqrt {10} }} = > f = \frac{1}{T} = \frac{{\sqrt {10} }}{\pi }(Hz)\) 5.11 Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hoà với biên độ góc \({\alpha _{\max }}\) nhỏ. Lấy mốc thế năng tại vị trí cân bằng. Tính li độ góc \(\alpha \) của con lắc khi nó chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng. Phương pháp giải: Thế năng của con lắc đơn : \({W_t} = mgl\frac{{{\alpha ^2}}}{2}\) Cơ năng của vật : \(W = {W_d} + {W_t} = \frac{1}{2}mgl\alpha _{\max }^2\) Lời giải chi tiết: Ta có cơ năng của vật \(W = {W_d} + {W_t} = \frac{1}{2}mgl\alpha _{\max }^2\) và \(Wd = {W_t}\) => \(2{W_t} = W = > 2.\left( {\frac{1}{2}mgl{\alpha ^2}} \right) = \frac{1}{2}mgl\alpha _{\max }^2 = > \alpha = \pm \frac{{\sqrt 2 }}{2}{\alpha _{\max }}\) Do con lắc đang chuyển động nhanh dần đều và chuyển động theo chiều dương => con lắc đi từ biên về VTCB => \(\alpha = - \frac{{\sqrt 2 }}{2}{\alpha _{\max }}\) 5.12 Một con lắc lò xo gồm một lò xo nhẹ có độ cứng k và một vật có khối lượng m = 100 g, được treo thằng đứng vào một giá cố định. Tại vị trí cân bằng O của vật, lò xo giãn 2,5 cm. Kéo vật dọc theo trục của lò xo xuống dưới cách vị trí cân bằng O một đoạn 2 cm rồi truyền cho nó vận tốc \(40\sqrt 3 \)cm/s theo phương thẳng đứng hướng xuống dưới. Chọn trục tọa độ Ox theo phương thẳng đứng, góc tại O, chiều dương hướng lên trên, gốc thời gian là lúc vật bắt đầu dao động. Lấy g = 10 \(m/{s^2}\). Biết chiều dài tự nhiên của của lò xo là 50 cm. a) Tính độ cứng của lò xo, viết phương trình dao động và tính cơ năng của vật. b) Xác định li độ và vận tốc của vật khi thế năng bằng \(\frac{1}{3}\) động năng. c) Tính thế năng, động năng và vận tốc của vật tại vị trí có li độ x= 2 cm. d) Tính chiều dài, lực đàn hồi cực đại, cực tiều của lò xo trong quá trình dao động. Phương pháp giải: Phương trình dao động điều hoà có dạng : \(x = A\cos \left( {\omega t + \varphi } \right)\) Cơ năng của vật dao động : \(W = \frac{1}{2}m{\omega ^2}{A^2}\) Động năng của vật dao động điều hòa : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Thế năng của vật dao động : \(\)\({W_t} = \frac{1}{2}m{\omega ^2}{x^2}\) Lực đàn hồi của lò xo : \(F = k.\Delta l\) Lời giải chi tiết: a) Tại VTCB ta có : \(mg = k.\Delta l = > k = \frac{{mg}}{{\Delta l}} = \frac{{0,1.10}}{{0,025}} = 40N/m\) => \(\omega = \sqrt {\frac{k}{m}} = 20rad/s\) Áp dụng công thức độc lập với thời gian ta được \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {2^2} + \frac{{{{40}^2}.3}}{{{{20}^2}}} = 16 = > A = 4cm\) Do ban đầu kéo vật xuống và truyền cho vật vận tốc hướng xuống nên vật tiếp tục chuyển động đi xuống dưới mà chiều dương của vật hướng lên nên ban đầu vật có li độ \(x = - 2\) và chuyển động theo chiều âm . \( = > \varphi = 180 - \arccos \frac{2}{4} = 120 = \frac{{2\pi }}{3}\) Phương trình dao động : \(x = 4\cos (20t + \frac{{2\pi }}{3})(cm/s)\) Cơ năng của vật dao động : \(W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,{1.20^2}.0,{04^2} = 0,032J\) b) Ta có \({W_d} = 3{W_t} = > \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = 3.\frac{1}{2}m{\omega ^2}{x^2} = > {A^2} - {x^2} = 3{x^2} = > 4{x^2} = {A^2} = > x = \pm \frac{A}{2}\) \( = > {v^2} = {20^2}({A^2} - \frac{{{A^2}}}{4}) = {20^2}.\frac{{3{A^2}}}{4} = {20^2}.\frac{{3.0,{{04}^2}}}{4} = 0,48 = > v = 0,69m/s\) c) Thay x=2 vào ta được \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}.0,{1.20^2}.(0,{04^2} - 0,{02^2}) = 0,024J\). \( = > v = 0,69m/s\) Thế năng của vật dao động \({W_t} = \frac{1}{2}m{\omega ^2}{x^2} = \frac{1}{2}.0,{1.20^2}.0,{02^2} = 0,008J\) d) Do \(A > \Delta l\)=> Vật có thể dãn có thể nén trong quá trình dao động => Lực đàn hồi dãn max khi vật ở vị trí thấp nhất : \({F_{dh\max }} = k.(\Delta l + A) = 50.(0,025 + 0,04) = 3,25(N)\) => Lực đàn hồi nén max khi vật ở vị trí cao nhất : \({F_{dh\max }} = k.(A - \Delta l) = 50.(0,04 - 0,025) = 0,75(N)\) => Lực đàn hồi min khi vật ở vị trí cân bằng => \({F_{dh\min }} = 0\) 5.13 Hãy phân tích sự chuyển hoá năng lượng giữa động năng và thế năng trong hệ gồm hai lò xo và vật nặng m được mắc như Hình 5.1. Khi quả nặng được thả cho dao động. Phương pháp giải: Vận dụng kiến thức về động năng của vật dao động điều hòa được xác định bởi biểu thức : \({W_d} = \frac{1}{2}m{\omega ^2}\left( {{A^2} - {x^2}} \right) = \frac{1}{2}m{v^2}\). Khi vật đi từ VTCB tới vị trí biên thì động năng của vật đang từ cực đại giảm đến 0. Khi vật đi từ vị trí biên về VTCB thì động năng của vật tăng từ 0 đến giá trị cực đại. Thế năng của vật dao động : \(\)\({W_t} = \frac{1}{2}m{\omega ^2}{x^2}\) Lời giải chi tiết: Hệ gồm 1 lò xo nén có thế năng đàn hồi , khi vật dao động thế năng giảm dần chuyển hóa thành động năng làm cho vật chuyển động đến VTCB thì \({W_t} = 0\), toàn bộ thế năng chuyển hóa thành động năng , sau đấy vật chuyển động chậm dần từ VTCB ra biên âm . Tại biên âm vật có \({W_d} = 0\), toàn bộ động năng đã chuyển hóa thành thế năng . Lò xo giãn chuyển đông ngược lại tương tự . Vật dao động điều hòa 5.14 Một người khối lượng 83 kg treo mình vào sợi dây bungee đàn hồi có độ cứng k= 270 N/m (Hình 5.2). Từ vị trí cân bằng người này được kéo đến vị trí mà sợi dây dãn thêm 5 m so với chiều dài tự nhiên và dao động điều hoà. Xác định vị trí và vận tốc của người này sau 2 s.
Phương pháp giải: Phương trình dao động điều hoà có dạng : \(x = A\cos \left( {\omega t + \varphi } \right)\) Chu kì dao động : \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta l}}{g}} \) Lực đàn hồi của lò xo : \(F = k.\Delta l\) Lời giải chi tiết: Tại VTCB ta có : \(\)\(mg = \Delta {l_0}.k = > \Delta {l_0} = \frac{{mg}}{k} \approx 3m\) Từ vị trí cân bằng người này được kéo đến vị trí mà sợi dây dãn thêm 5 m so với chiều dài tự nhiên và dao động điều hoà. => \(A + \Delta {l_0} = 5 = > A = 2m\) Vận tốc góc \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{270}}{{83}}} (rad/s)\) Ta có pt chuyển động của vật \(x = A\cos \left( {\omega t} \right) = 2\cos \left( {\sqrt {\frac{{270}}{{83}}} t} \right)\) Thay t = 2 vào pt ta có \(\)\(x = 2\cos \left( {\sqrt {\frac{{270}}{{83}}} .2} \right) \approx - 1,8m\) Áp dụng công thức độc lập với thời gian ta có \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{A^2}{\omega ^2}}} = 1 = > v = 1.57m/s\)
|