Bài 9. Sóng ngang, sóng dọc, sự truyền năng lượng của sóng cơ trang 19, 20 SBT Vật lí 11 Kết nối tri thức với cuộc sống

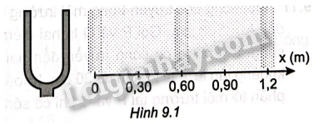
9.1

Chọn câu đúng.

A. Sóng dọc là sóng truyền dọc theo một sợi dây.

B. Sóng dọc là sóng truyền theo phương thẳng đứng, còn sóng ngang là sóng truyền theo phương nằm ngang.

C. Sóng dọc là sóng trong đó phương dao động (của các phần tử môi trường) trùng với phương truyền.

D. Sóng ngang là sóng trong đó phương dao động (của các phần tử môi trường) trùng với phương truyền.

Phương pháp giải:

Sử dụng khái niệm của sóng dọc và sóng ngang

Lời giải chi tiết:

Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang.

Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng gọi là sóng dọc.

Đáp án : C

9.2

Tìm phát biểu sai khi nói về sóng cơ.

A. Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha nhau.

B. Sóng trong đó các phần tử môi trường dao động theo phương trùng với phương truyền sóng được gọi là sóng dọc.

C. Tại mỗi điểm của môi trường có sóng truyền qua, biên độ của sóng là biên độ dao động của phần tử môi trường.

D. Sóng trong đó các phần tử môi trường dao động theo phương vuông góc với phương truyền sóng được gọi là sóng ngang.

Phương pháp giải:

Sử dụng khái niệm của sóng dọc và sóng ngang

Bước sóng  là khoảng cách giữa hai ngọn sóng liên tiếp

Lời giải chi tiết:

Khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha nhau là \(d = \left( {2k + 1} \right)\frac{\lambda }{2}\)

Đáp án : A

9.3

Sóng cơ không truyền được trong

A. chân không.

B. không khí.

C.nước.

D. kim loại.

Phương pháp giải:

Tính chất của sóng cơ

Lời giải chi tiết:

Sóng cơ truyền được trong môi trường vật chất rắn , lỏng , khí .

Đáp án :A

9.4

Một sóng ngang có tần số 100 Hz truyền trên một sợi dây nằm ngang với tốc độ 60 m/s, qua điểm A rồi đến điểm B cách nhau 7,95 m. Tại một thời điểm nào đó A có li độ âm và đang chuyển động đi lên thì điểm B đang có li độ

A. âm và đang đi xuống.

B. âm và đang đi lên.

C. dương và đang đi lên.

D. dương và đang đi xuống.

Phương pháp giải:

Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda }\)

Bước sóng của dao động : \(\lambda  = v.T = \frac{v}{f}\)

Lời giải chi tiết:

Ta có bước sóng của dao động : \(\lambda  = v.T = \frac{v}{f} = \frac{{60}}{{100}} = 0,6m\)

Độ lệch pha giữa 2 điểm A và B trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda } = \frac{{2\pi AB}}{\lambda } = \frac{{2\pi .7,95}}{{0,6}} = 26\pi  + \frac{\pi }{2} = \frac{\pi }{2}\)

Do sóng truyền từ A đến B nên A sớm pha hơn B một góc \(\frac{\pi }{2}\)

=> Tại một thời điểm nào đó A có li độ âm và đang chuyển động đi lên thì điểm B đang có li độ âm và đang đi xuống

Đáp án : A

9.5

Mũi tên nào trong Hình 9.1 mô tả đúng hướng truyền dao động của các phần tử môi trường?

A. \( \uparrow \)

B. \( \downarrow \)

C. \( \to \)

D. \( \leftrightarrow \)

Phương pháp giải:

Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang.

Lời giải chi tiết:

Từ hình ta nhận thấy đây là sóng ngang => các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng

Đáp án : A

9.6

Nếu tốc độ truyền sóng âm trong Hình 9.1 là 340 m/s thì tần số của sóng khoảng

A. 566,7 Hz.

B. 204 Hz.

C. 0,00176 Hz.

D. 0,176 Hz.

Phương pháp giải:

Khoảng cách hai điểm trên cùng một phương truyền sóng luôn dao động cùng pha nhau là \(d = k\lambda \)

Bước sóng là khoảng cách giữa hai ngọn sóng liên tiếp :\(\lambda  = v.T = \frac{v}{f}\)

Lời giải chi tiết:

Khoảng cách hai điểm gần nhau nhấttrên cùng một phương truyền sóng luôn dao động cùng pha nhau là \(1\lambda  =  > \lambda  = 0,6m =  > f = \frac{v}{\lambda } = 566,7Hz\)

9.7

Một sóng ngang truyền trên một sợi dây rất dài từ P đến Q. Hai điểm P, Q trên phương truyền sóng cách nhau \(PQ = \frac{{5\lambda }}{4}\) .  Kết luận nào sau đây là đúng?

A. Khi P có li độ cực đại thì Q có vận tốc cực đại.

B. Li độ P, Q luôn trái dấu.

C. Khi Q có li độ cực đại thì P có vận tốc cực đại.

D. Khi P có li độ cực đại thì Q qua vị trí cân bằng theo chiều âm. Khi Q có li độ cực đại thì P qua vị trí cân bằng theo chiều dương.

Phương pháp giải:

Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda }\)

Lời giải chi tiết:

P sớm pha hơn Q một góc \(\Delta \varphi  = \frac{{2\pi d}}{\lambda } = 2,5\pi (rad)\)=> P và Q vuông pha nhau

=> Khi P có Khi P có li độ cực đại thì Q có vận tốc cực đại

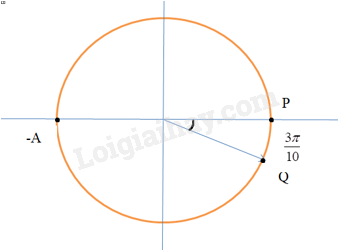
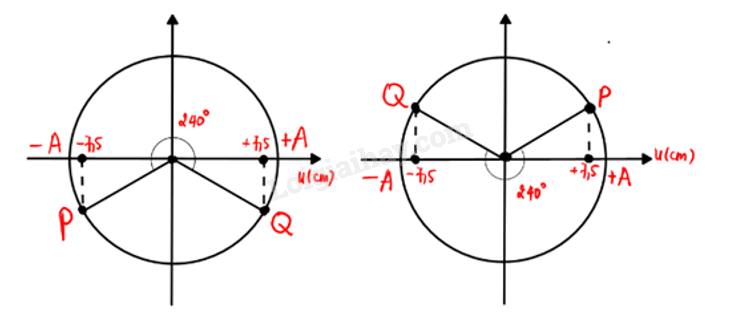
Đáp án : A

9.8

Một sóng cơ có tần số 20 Hz truyền trên mặt nước với tốc độ 1,5 m/s. Trên phương truyền sóng, sóng truyền tới điểm P rồi mới tới điểm Q cách nó 16,125 cm. Tại thời điểm t , điểm P hạ xuống thấp nhất thì sau thời gian ngắn nhất là bao nhiêu điểm Q sẽ hạ xuống thấp nhất?

Phương pháp giải:

Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda }\)

Bước sóng của dao động : \(\lambda  = v.T = \frac{v}{f}\)

Sử dụng vòng tròn lượng giác

Lời giải chi tiết:

Ta có : \(\lambda  = \frac{v}{f} = \frac{{1,5}}{{20}} = 7,5cm\)

Chu kì \(T = \frac{1}{f} = \frac{1}{{20}} = 0,05s\)

Độ lệch pha giữa 2 điểm P và Q là : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda } = \frac{{2\pi .16,125}}{{7,5}} = \frac{{43\pi }}{{10}} = 4\pi  + \frac{{3\pi }}{{10}}\)

=> P sớm pha hơn Q một góc \(\varphi  = \frac{{3\pi }}{{10}}\)

Tại thời điểm t , điểm P hạ xuống thấp nhất thì sau thời gian ngắn nhất để điểm Q sẽ hạ xuống thấp nhất là \(t = \frac{{3T}}{{20}} + \frac{T}{2} = \frac{{13T}}{{20}} = 0,0325s\)

9.9

Hình 9.2 mô tả một phần của sóng dọc truyền trên một sợi dây lò xo. Hãy nêu cách xác định bước sóng của sóng này và chỉ ra điểm tương đồng của nó với  sóng âm truyền trong không khí.

Phương pháp giải:

Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng gọi là sóng dọc.

Lời giải chi tiết:

Khoảng cách hai điểm gần nhau nhấttrên cùng một phương truyền sóng luôn dao động cùng pha nhau là \(1\lambda \)
Điểm tương đồng của nó với  sóng âm truyền trong không khí là : sóng âm truyền trong không khí là sóng dọc.

9.10

P và Q là hai điểm trên mặt nước cách nhau một khoảng 20 cm. Tại một điểm O trên đường thẳng PQ và nằm ngoài đoạn PQ, người ta đặt nguồn dao động điều hoà theo phương vuông góc với mặt nước với phương trình \(u = 5\cos \omega t(cm)\), tạo ra sóng trên mặt nước với bước sóng \(\lambda  = 15\) cm. Khoảng cách xa nhất và gần nhất giữa hai phần tử môi trường tại P và Q khi có sóng truyền qua là bao nhiêu?

Phương pháp giải:

Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda }\)

Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)

Lời giải chi tiết:

Giả sử P gần nguồn hơn lúc này P nhanh pha hơn Q một góc bằng

\(\Delta \varphi  = \frac{{2\pi d}}{\lambda } = \frac{{2\pi {d_{PQ}}}}{\lambda } = \frac{{2\pi }}{3}\)

Phương trình sóng tại P và Q lần lượt là :

\({u_P} = 5\cos \left( {\omega t - \frac{{2\pi {d_{OP}}}}{{15}}} \right)\)

\({u_Q} = 5\cos \left( {\omega t - \frac{{2\pi {d_{OP}}}}{{15}} - \frac{{2\pi }}{3}} \right)\)

=> \(\Delta u = {u_P} - {u_Q} = 5\sqrt 3 \cos \left( {\omega t - \frac{{2\pi {d_{OP}}}}{{15}} - \frac{{5\pi }}{6}} \right) =  > \Delta {u_{\max }} = 5\sqrt 3 \)

=> \({d_{\max }} = \sqrt {{{20}^2} + {{\left( {5\sqrt 3 } \right)}^2}}  \approx 21,79cm\)

=> \({d_{\min }} = PQ = 20cm\)

9.11

Một sóng dọc truyền trong môi trường với bước sóng 15 cm, biên độ không đổi \(A = 5\sqrt 3 \) cm. Gọi P và Q là hai điểm cùng nằm trên một phương truyền sóng. Khi chưa có sóng truyền đến hai điểm P và Q nằm cách nguồn các khoảng lần lượt là 20 cm và 30 cm. Khoảng cách xa nhất và gần nhất giữa hai phần tử môi trường tại P và Q khi có sóng truyền qua là bao nhiêu ?

Phương pháp giải:

Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi  = \frac{{2\pi d}}{\lambda }\)

Lời giải chi tiết:

Độ lệch pha dao động giữa 2 điểm PQ : \(\Delta \varphi  = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi 10}}{{15}} = \frac{{4\pi }}{3}\)

=> Khoảng cách giữa hai điểm P và Q là : \(d = \Delta x + \Delta {x_\varphi }\)với \(\Delta {x_\varphi }\)là khoảng cách thêm vào do sự dao động dọc theo phương truyền sóng .

Từ hình vẽ ta có : \({l_{\max }} = 25cm\) (ứng với P chuyển động tới vị trí \({u_P} = \frac{{ - A\sqrt 3 }}{2}\) theo chiều dương và Q đến vị trí \({u_Q} = \frac{{ + A\sqrt 3 }}{2}\) theo chiều dương )

\({l_{\min }} = 0\)(ứng với P chuyển động tới vị trí \({u_P} = \frac{{A\sqrt 3 }}{2}\) theo chiều âm  và Q đến vị trí \({u_Q} = \frac{{A\sqrt 3 }}{2}\) theo chiều âm)