Bài 6. Phản xạ toàn phần trang 16, 17, 18 SBT Khoa học tự nhiên 9 Kết nối tri thứcKhi ánh sáng truyền từ môi trường có chiết suất n1 tới môi trường có chiết suất n2 thì điều kiện để xảy ra phản xạ toàn phần tại mặt phân cách giữa hai môi trường này là:
Lựa chọn câu để xem lời giải nhanh hơn
6.1 Khi ánh sáng truyền từ môi trường có chiết suất n1 tới môi trường có chiết suất n2 thì điều kiện để xảy ra phản xạ toàn phần tại mặt phân cách giữa hai môi trường này là: A. Chỉ cần n1 > n2 B. Chỉ cần góc tới lớn hơn hoặc bằng góc tới hạn: i ≥ ith C. n1 > n2 và góc tới lớn hơn hoặc bằng góc tới hạn: i ≥ ith D. n1 > n2 và góc tới nhỏ hơn hoặc bằng góc tới hạn: i ≤ ith Phương pháp giải: Vận dụng kiến thức về hiện tượng phản xạ toàn phần. Lời giải chi tiết: Khi ánh sáng truyền từ môi trường có chiết suất n1 tới môi trường có chiết suất n2 thì điều kiện để xảy ra phản xạ toàn phần tại mặt phân cách giữa hai môi trường này là: n1 > n2 và góc tới lớn hơn hoặc bằng góc tới hạn: i ≥ ith Đáp án: C 6.2 Ghép nội dung ở cột bên trái với nội dung tương ứng ở cột bên phải để có một phát biểu đúng và đầy đủ.
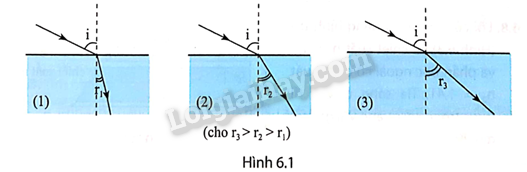
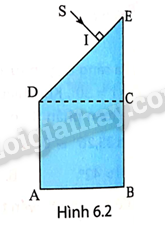
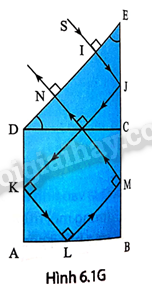
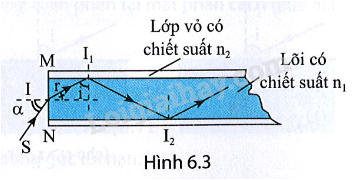
Phương pháp giải: Vận dụng kiến thức về ánh sáng. Lời giải chi tiết: 1-b, 2-e, 3-d, 4-c 6.3 Tia sáng truyền từ không khí vào chất lỏng với góc tới i = 60° thì góc khúc xạ r = 30°. Khi chiếu tia sáng đó từ chất lỏng ra không khí, muốn có phản xạ toàn phần thì góc tới i phải thoả mãn điều kiện nào dưới đây? Cho biết sin 35,26°≈ 0,58. A. i > 42°. B. i < 42°. C. i > 35,26°. D. i > 28,5°. Phương pháp giải: Vận dụng kiến thức về hiện tượng phản xạ toàn phần. Lời giải chi tiết: Ta có: n2=n1sinisinr=1.sin60sin30=√3 Muốn có phản xạ toàn phần thì i > ith mà sinith=n2n1=1√3→ith=35.26o nên i > 35,26°. Đáp án: C 6.4 Có tia sáng truyền từ không khí vào ba môi trường (1), (2), (3) như Hình 6.1. Phản xạ toàn phần có thể xảy ra khi ánh sáng truyền trong cặp môi trường nào sau đây? A. Từ (2) tới (1). B. Từ (1) tới (2). C. Từ (3) tới (1). D. Từ (3) tới (2). Phương pháp giải: Vận dụng kiến thức về hiện tượng phản xạ toàn phần. Lời giải chi tiết: Vì r3 > r2 > r1 nên n3 < n2 < n1 . Vậy phản xạ toàn phần có thể xảy ra khi ánh sáng truyền trong cặp môi trường từ (1) tới (2). Đáp án: B 6.5 Ba môi trường trong suốt là không khí và hai môi trường khác có các chiết suất tuyệt đối n1, n2 (với n2 > n1). Lần lượt cho ánh sáng truyền đến mặt phân cách của tất cả các cặp môi trường có thể tạo ra. Biểu thức nào sau đây không thể là sin của góc tới hạn ith đối với cặp môi trường tương ứng? A. n2n1 B. 1n1 C. 1n2 D. n1n2 Phương pháp giải: Vận dụng kiến thức về chiết suất tỉ đối giữa 2 môi trường Lời giải chi tiết: 1n1 không thể là sin của góc tới hạn ith đối với cặp môi trường tương ứng Đáp án: A 6.6 Có ba môi trường trong suốt (1), (2) và (3). Với cùng một góc tới, nếu ánh sáng đi từ môi trường (1) vào môi trường (2) thì góc khúc xạ là 30°, nếu ánh sáng đi từ môi trường (1) vào môi trường (3) thì góc khúc xạ là 45°. Cho biết sin 30° = 0,5; sin 45° = √22 a) Trong hai môi trường (2) và (3), tốc độ ánh sáng truyền trong môi trường nào lớn hơn? b) Tính góc tới hạn phản xạ toàn phần giữa hai môi trường (2) và (3). Phương pháp giải: Vận dụng kiến thức về định luật khúc xạ ánh sáng và phản xạ ánh sáng. Lời giải chi tiết: a) n1sini = n2sin30° = n3sin45° ⇒n2n3=sin45osin30o=√2>1 Vì n2 > n3 nên v3 > v2 tốc độ ánh sáng truyền trong môi trường (3) lớn hơn môi trường (2). b) sinith=sin30osin45o=2√2⇒ith=45o 6.7 Một khối thuỷ tinh có tiết diện thẳng như Hình 6.2 đặt trong không khí, ABCD là hình vuông, CDE là tam giác vuông cân. Trong mặt phẳng của tiết diện thẳng, chiếu một chùm tia sáng đơn sắc hẹp SI vuông góc với DE (IE < ID). Biết chiết suất của thuỷ tinh là n = 1,5. Vẽ đường đi của tia sáng trong khối thuỷ tinh. Phương của tia ló hợp với pháp tuyến của mặt mà tia sáng ló ra một góc bằng bao nhiêu độ? Phương pháp giải: Vận dụng kiến thức về sự phản xạ ánh sáng. Lời giải chi tiết: Tia SI truyền thẳng tới mặt EC tại J. Ta có: sinith=1n=23⇒ith≈42o Đường truyền của tia sáng được mô tả trên Hình 6.1G. Góc tới tại điểm J: iJ = 45° > ith nên có phản xạ toàn phần. Tia phản xạ từ J sẽ lần lượt phản xạ toàn phần tại K, L, M trên DA, AB, BC rồi ló ra khỏi DE ở N theo phương vuông góc với DE. Do đó, MN//SI, tức là MN hợp với pháp tuyển của DE một góc là 0°. 6.8 Lõi của một sợi quang hình trụ (Hình 6.3) có chiết suất n1 = 1,5 và phần bọc ngoài có chiết suất n2=1,41. Tia sáng truyền đi bằng được trong sợi quang với góc tới α=29°.
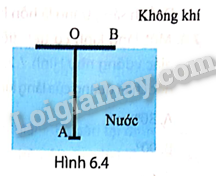
a) Tính các góc r và i b) Tính góc tới hạn phản xạ toàn phần giữa lớp vỏ và lõi. Phương pháp giải: Vận dụng kiến thức về sự phản xạ ánh sáng. Lời giải chi tiết: a) Ta có: sinr=sinαn1=sin29o1,5=0,32⇒r=18,66o⇒i=71,34o b) sinith=n2n1=1,411,5⇒ith≈70,05o 6.9 Một cái đinh được cắm vuông góc vào tâm O của một tấm gỗ hình tròn có bán kính R = 0,05 m. Tấm gỗ được thả nổi trên mặt thoáng của một chậu nước (Hình 6.4). Đầu A của đinh ở trong nước. Cho chiết suất của nước là n = 43
a) Cho chiều dài OA của đinh ở trong nước là 8,7 cm. Hỏi đặt mắt ở trong không khí nhìn đầu đinh theo phương đi sát mép gỗ sẽ thấy đầu đinh ở cách mặt nước một khoảng bao nhiêu? b) Cho chiều dài OA giảm dần. Xác định khoảng cách OA để mắt không còn nhìn thấy đầu A của định. Phương pháp giải: Vận dụng kiến thức về sự phản xạ ánh sáng. Lời giải chi tiết: a) Theo Hình 6.2G ta có: tanα=OAR=8,75≈1,73⇒α≈60o⇒i=90o−α=30o sinr=nsini=43sin30o=23⇒r=41,8o Vậy tanr = tan 41,8° ≈ 0,89 Lại có: tanr=OBOA′⇒OA′=OBtan41,8o=0,05tan41,8o≈0,056(m) b) Theo Hình 6.3G, nếu cho chiều dài OA giảm dần thì góc tới i sẽ tăng dần. Khi i≥ith thì tia sáng sẽ phản xạ toàn phần, không có tia khúc xạ ló ra không khí. Khi đó, mắt không còn nhìn thấy đầu A của đinh nữa: sinith=1n=34⇒ith≈48,6o Từ Hình 6.3G, ta xác định được: OA=OBtan(^OAB)=OBtanith=OBtan48,6o=51,13≈4,4(cm)
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|