Giải mục 3 trang 73, 74 SGK Toán 9 tập 2 - Cùng khám pháBạn Thiện có một phễu đong dạng hình nón (Hình 9.25a) và một thùng không chứa dạng hình trụ (Hình 9.25b) với cùng bán kính đáy r và chiều cao h. Thiện dùng phễu đong đày nước rồi đổ vào thùng chứa thì thấy rằng mực nước bằng \(\frac{1}{3}\) chiều cao của thùng. a) Tính thể tích V của phần nước trong thùng chứa theo r và h. b) Hãy dự đoán thể tích của phễu đong.
Lựa chọn câu để xem lời giải nhanh hơn
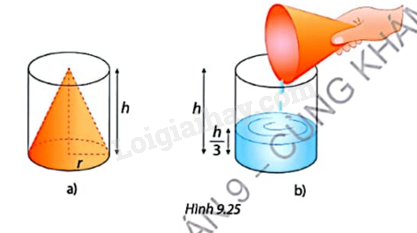
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 73 SGK Toán 9 Cùng khám phá Bạn Thiện có một phễu đong dạng hình nón (Hình 9.25a) và một thùng không chứa dạng hình trụ (Hình 9.25b) với cùng bán kính đáy r và chiều cao h. Thiện dùng phễu đong đày nước rồi đổ vào thùng chứa thì thấy rằng mực nước bằng \(\frac{1}{3}\) chiều cao của thùng. a) Tính thể tích V của phần nước trong thùng chứa theo r và h. b) Hãy dự đoán thể tích của phễu đong.
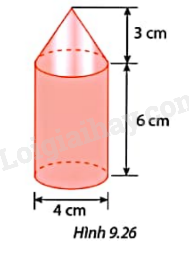
Phương pháp giải: Dựa theo thể tích hình trụ: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ). Lời giải chi tiết: a) Thể tích của phần nước trong thùng là: \(V = \pi {r^2}\frac{h}{3}\). b) Thể tích của phễu đong bằng \(\frac{1}{3}\) thể tích hình trụ. LT3 Trả lời câu hỏi Luyện tập 3 trang 73 SGK Toán 9 Cùng khám phá Một hình nón có đường sinh bằng 10 cm và chiều cao bằng 8 cm. Tính thể tích của hình nón. Phương pháp giải: Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón). Lời giải chi tiết: Bán kính đáy của hình nón là: \(\sqrt {{{10}^2} - {8^2}} = 6\) cm Thể tích hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \) (cm3). VD3 Trả lời câu hỏi Vận dụng 3 trang 74 SGK Toán 9 Cùng khám phá Tính thể tích của mô hình tên lửa trong Hình 9.26.
Phương pháp giải: Thể tích hình trụ: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ). Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón). Lời giải chi tiết: Thể tích hình trụ là: \(V = \pi {r^2}h = \pi {.2^2}.6 = 24\pi \) (cm3). Thể tích hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.2^2}.3 = 4\pi \)(cm3). Thể tích của mô hình tên lửa là: \(24\pi + 4\pi = 28\pi \)(cm3).
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|