Giải mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạoÔng An có một bể kính hình lập phương như Hình 2. Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính). a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức: a3 = ? hay a = ?. b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai). Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Lựa chọn câu để xem lời giải nhanh hơn
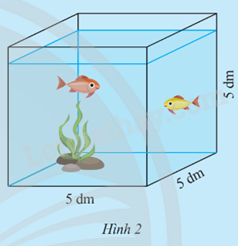
HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 9 Chân trời sáng tạo Ông An có một bể kính hình lập phương như Hình 2.
Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính). a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức: a3 = ? hay a = ?. b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai). Phương pháp giải: - Sử dụng công thức thể tích lập phương V = cạnh.cạnh.cạnh - Thay lần lượt giá trị n để tính. Lời giải chi tiết: a) a3 = (5.5.5).n = 125n hay a = . b) Khi n = 8, ta được: a = Khi n = 4, ta được: a = . TH4 Video hướng dẫn giải Trả lời câu hỏi Thực hành 4 trang 44 SGK Toán 9 Chân trời sáng tạo Cho biểu thức Q = . Tính giá trị của Q khi x = 2 và khi x = - 3 (kết quả làm tròn đến chữ số thập phân thứ hai). Phương pháp giải: Thay lần lượt giá trị của x vào biểu thức Q để tính. Lời giải chi tiết: Khi x = 2 suy ra Q = . Khi x = - 3 suy ra Q = .
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|