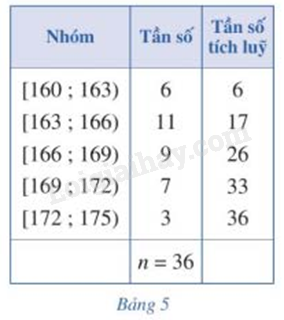
Giải mục 2 trang 86,87 SGK Toán 12 tập 1 - Cánh diềuKhoảng tứ phân vị Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Trả lời câu hỏi Hoạt động 2 trang 86 SGK Toán 12 Cánh diều Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.
a) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{36}}{4} = 9\) có đúng không? Tìm đầu mút trái s, độ dài h, tần số \({n_2}\) của nhóm 2; tần số tích lũy của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất của mẫu số liệu đã cho theo công thức sau: \({Q_1} = s + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).h\) b) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{2} = \frac{{36}}{2} = 18\) có đúng không? Tìm đầu mút trái r, độ dài d, tần số của nhóm 3; tần số tích lũy của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai của mẫu số liệu đã cho theo công thức sau: \({Q_2} = r + \left( {\frac{{18 - c{f_2}}}{{{n_3}}}} \right).d\) c) Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.36}}{4} = 27\) có đúng không? Tìm đầu mút trái t, độ dài l, tần số của nhóm 4; tần số tích lũy của nhóm 3. Sau đó, hãy tính tứ phân vị thứ ba của mẫu số liệu đã cho theo công thức sau:\({Q_3} = t + \left( {\frac{{27 - c{f_3}}}{{{n_4}}}} \right).l\) d) Tìm hiệu \({Q_3} - {Q_1}\) Phương pháp giải - Xem chi tiết Quan sát bảng số liệu Lời giải chi tiết a) Đúng vì tần số tích lũy của nhóm 2 là 17 > 9 s = 163; h = 166 – 163 = 3; \({n_2} = 11\); \(c{f_1} = 6\) \({Q_1} = s + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).h = 163 + \left( {\frac{{9 - 6}}{{11}}} \right).3 = \frac{{1802}}{{11}}\) b) Đúng vì tần số tích lũy của nhóm 3 là 26 > 18 r = 166; d = 169 – 166 = 3; \({n_3} = 9\); \(c{f_2} = 17\) \({Q_2} = r + \left( {\frac{{18 - c{f_2}}}{{{n_3}}}} \right).d = 166 + \left( {\frac{{18 - 17}}{9}} \right).3 = \frac{{499}}{3}\) c) Đúng vì tần số tích lũy của nhóm 4 là 33 > 27 t = 169; l = 172 – 169 = 3; \({n_4} = 7\); \(c{f_3} = 26\) \({Q_3} = t + \left( {\frac{{27 - c{f_3}}}{{{n_4}}}} \right).l = 169 + \left( {\frac{{27 - 26}}{7}} \right).3 = \frac{{1186}}{7}\) d) \({Q_3} - {Q_1} = \frac{{1186}}{7} - \frac{{1802}}{{11}} = \frac{{432}}{{77}}\)
|