Giải mục 2 trang 58,59,60 SGK Toán 12 tập 1 - Cánh diều

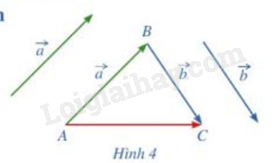
HĐ2

Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều

Trong không gian, cho 2 vec tơ $\vec a$ và $\vec b$. Lấy một điểm A tùy ý.

a) Vẽ $\overrightarrow {AB}$$= \vec a$,$\overrightarrow {BC}$$= \vec b$

b) Tổng của 2 vec tơ $\vec a$và$\vec b$ bằng vec tơ nào trong hình 4?

Phương pháp giải:

a) Ghi rõ các bước để vẽ hình

b) Áp dụng quy tắc 3 điểm $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$

Lời giải chi tiết:

a)

– Qua A vẽ một đường thẳng song song với $\vec a$. Trên đường thẳng đó lấy điểm B sao cho $AB = \left| {\vec a} \right|$ và $\overrightarrow {AB}$ cùng hướng với ${\vec a}$.

– Qua B vẽ một đường thẳng song song với $\vec b$. Trên đườ ng thẳng đó lấy điểm C sao cho $BC = \left| {\vec b} \right|$ và $\overrightarrow {BC}$ cùng hướng với ${\vec b}$.

b) Ta có: $\vec a + \vec b = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$

Quảng cáo

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa $\overrightarrow {AB}  + \overrightarrow {AD}$ và  $\overrightarrow {AC} ;\;\overrightarrow {AC}  + \overrightarrow {AA'}$ và $\overrightarrow {AC'}$.

Phương pháp giải:

Áp dụng quy tắc ba điểm.

Lời giải chi tiết:

Áp dụng quy tắc ba điểm ta thấy:

$\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {BD}$               (1)

Mà từ hình vẽ ta thấy  $\overrightarrow {BD}  = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)$

Từ (1) (2) => $\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$

$\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {A'C}$                  (3)

Mà $\overrightarrow {A'C}  = \overrightarrow {AC'}$                     (4)

Từ (3), (4) suy ra $\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'}$

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều

Trong không gian , cho hai vecto$\;\vec a,\vec b.\;$ Lấy một điểm M tùy ý.

a) Vẽ $\overrightarrow {MA}  = \vec a,\;\overrightarrow {MB}  = \vec b\;,\overrightarrow {MC}  = \overrightarrow { - b}$.

b) Tổng của hai vecto $\vec a\;$và $\;\overrightarrow { - b}$ bằng vecto nào trong hình 7.

Phương pháp giải:

Sử dụng quy tắc hình bình hành.

Lời giải chi tiết:

$\vec{a}$ + ($- \vec{b}) =$ $\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MN}$ (quy tắc hình bình hành).

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều

Nêu định nghĩa tích của một số thực $k \ne 0\;$với vecto$\;\vec a\; \ne \vec 0$ trong mặt phẳng.

Lời giải chi tiết:

Cho số thực $k \ne 0$ và $vecto\;\vec a \ne \vec 0$. Tích của số k với vecto $\vec a$ là một vecto, kí hiệu là $k\vec a,\;$được xác định như sau:

- Cùng hướng với vecto $\vec a$ nếu k > 0, ngược hướng với vecto $\vec a$ nếu k < 0.

- Có độ dài bằng $\left| k \right|.\left| {\vec a} \right|$.

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hai vecto $\vec a,\vec b$khác $\;\vec 0$. Lấy một điểm O tùy ý.

a) Vẽ hai vecto $\overrightarrow {OA}  = \vec a,\;\overrightarrow {OB}  = \vec b$

b) Khi đó , hai vecto $\overrightarrow {OA}, \overrightarrow {OB}$ có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto $\overrightarrow {OA}, \;\overrightarrow {OB}$ trong hai mặt phẳng (P).

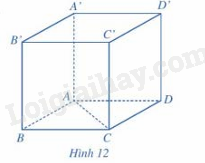
Lời giải chi tiết:

Trong không gian, cho hai vecto $\vec a, \vec b$ khác $\;\vec 0$. Lấy một điểm O tùy ý và vẽ hai vecto$\;\overrightarrow {OA}  = \vec a,\overrightarrow {OB}  = \vec b$. Góc giữa hai vecto $\vec a,\overrightarrow {b\;}$ trong không gian, ký hiệu $\left( {\vec a,\vec b} \right)$ là góc giữa hai vecto $\;\overrightarrow {OA} ,\overrightarrow {OB}$.

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12).

a) Tính góc giữa hai vecto $\overrightarrow {AC} ,\overrightarrow {A'D'}$.

b) Tính $\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|$. Cos($\overrightarrow {AC} ,\overrightarrow {A'D'}$).

Phương pháp giải:

Áp dụng quy tắc 3 điểm và vectơ trong không gian.

Lời giải chi tiết:

Ta có A’D’//AD.

Góc giữa $\overrightarrow {AC} \;$và$\;\overrightarrow {A'D'}$= $\;\overrightarrow {AC}$ và $\overrightarrow {AD}$.

a) Mà ABCD là hình vuông => $\widehat {CAD} = 45^\circ$

b) $\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|}$ = AC.AD = 3.3 = 9.

cos($\overrightarrow {AC} ,\overrightarrow {A'D'}$)= cos($\overrightarrow {AC} ,\overrightarrow {AD} )$= $\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1$.