Giải mục 2 trang 46, 47 SGK Toán 11 tập 2 - Cùng khám pháMột vật chuyển động thẳng với phương trình \(s\left( t \right) = {t^3} + t\), với \(s\) tính bằng mét và \(t\) tính bằng giây
Lựa chọn câu để xem lời giải nhanh hơn
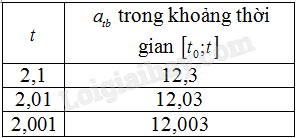
Hoạt động 2 Một vật chuyển động thẳng với phương trình \(s\left( t \right) = {t^3} + t\), với \(s\) tính bằng mét và \(t\) tính bằng giây a) Tính vận tốc của vật tại thời điểm \(t\). b) Cho biết gia tốc trung bình (đơn vị \(m/{s^2}\)) của vật trong khoảng thời gian \(\left[ {{t_0};t} \right]\) được tính bởi công thức \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}}\). Hãy tính gia tốc trung bình trong các khoảng thời gian \(\left[ {{t_0};t} \right]\) với \({t_0} = 2\) và \(t\) lần lượt là \(2,1\); \(2,01\); \(2,001\). Sau đó, hoàn thành Bảng 7.3.
Phương pháp giải: a) \(v\left( t \right) = s'\left( t \right)\); công thức tính đạo hàm \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\) b) Tính \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}}\). Sau đó thay \(t\) và \({t_0}\) vào \({a_{tb}}\) Lời giải chi tiết: a) Vận tốc của vật tại thời điểm \(t\) là \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} + t} \right)' = 3{t^2} + 1\) b) \(v\left( t \right) - v\left( {{t_0}} \right) = \left( {3{t^2} + 1} \right) - \left( {3t_0^2 + 1} \right) = 3\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)\) Suy ra \({a_{tb}} = \frac{{v\left( t \right) - v\left( {{t_0}} \right)}}{{t - {t_0}}} = 3\left( {t + {t_0}} \right)\) tại \({t_0} = 2\) là \({a_{tb}} = 3\left( {t + 2} \right)\) +) Với \(t = 2,1\) ta có \({a_{tb}} = 3.\left( {2,1 + 2} \right) = 12,3\) +) Với \(t = 2,01\) ta có \({a_{tb}} = 3.\left( {2,01 + 2} \right) = 12,03\) +) Với \(t = 2,001\) ta có \({a_{tb}} = 3.\left( {2,001 + 2} \right) = 12,003\) Vậy ta có bảng sau
Luyện tập 2 Phương trình chuyển động của một con lắc lò xo dao động quanh vị trí cân bằng \(O\) là \(x = 4\cos 2t\), trong đó \(t\) tính bằng giây và \(x\) tính bằng \(cm\). Tính gia tốc của con lắc tại thời điểm \(t\). Phương pháp giải: +) \(a\left( t \right) = x''\left( t \right)\) +) \(\left( {\cos u} \right) = - u'.\sin u;\,\,\,\left( {\sin u} \right) = u'.\cos u\) Lời giải chi tiết: Ta có \(x' = \left( {4\cos 2t} \right)' = - 4.\sin 2t.\left( {2t} \right)' = - 8\sin 2t\) \(a\left( t \right) = x'' = - 8.\cos 2t.\left( {2t} \right)' = - 16\cos 2t\)
|