Giải mục 2 trang 34,35,36 SGK Toán 12 tập 2 - Cánh diều

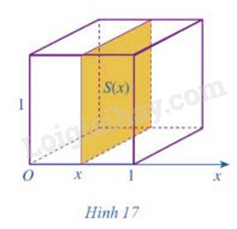
HĐ3

Trả lời câu hỏi Hoạt động 3 trang 34 SGK Toán 12 Cánh diều

Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ta nhận được hình phẳng có diện tích là S(x) (Hình 17)

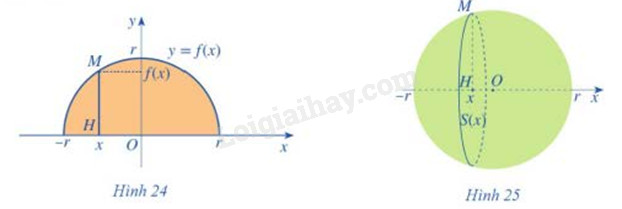
a) Tính S(x)

b) So sánh thể tích khối lập phương đó với \(\int\limits_0^1 {S(x)dx} \)

Phương pháp giải:

Sử dụng công thức tính diện tích hình vuông, thể tích hình lập phương và tích phân

Lời giải chi tiết:

a)  S(x) = 1

b) Thể tích khối lập phương V = 1

\(\int\limits_0^1 {S(x)dx}  = \int\limits_0^1 {1dx}  = 1\)

Vậy thể tích khối lập phương đó = \(\int\limits_0^1 {S(x)dx} \)

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 37 SGK Toán 12 Cánh diều

Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)

a) Tìm hàm số y = f(x)

b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) \(( - r \le x \le r)\) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)

Tính diện tích S(x) của hình tròn đó theo f(x)

Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r

Phương pháp giải:

a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn

b) Sử dụng công thức tính thể tích hình cầu

Lời giải chi tiết:

a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r

\( \Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}} \)

b) \(S(x) = \pi {f^2}(x)\)

\(V = \frac{{4\pi {r^3}}}{3}\)