Giải mục 1 trang 84, 85, 86 SGK Toán 9 tập 2 - Kết nối tri thức

HĐ1

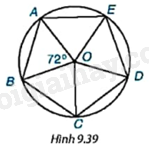
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9 Kết nối tri thức

Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:

- Vẽ đường tròn tâm O bán kính R.

- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).

Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).

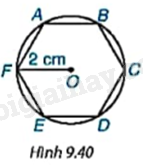
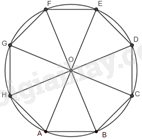
Phương pháp giải:

+ Chứng minh được các tam giác \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\)

Suy ra: \(AE = ED = DC = CB = BA\) và

\(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)

+ Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\)

Lời giải chi tiết:

Vì đa giác ABCDE nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE\).

Theo giả thiết: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = {72^o}\)

Do đó, \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\).

Suy ra:

+) \(AE = ED = DC = CB = BA\)

+) \(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)

Do đó, \(\widehat {OAE} + \widehat {OAB} = \widehat {OEA} + \widehat {OED} = \widehat {ODE} + \widehat {ODC} = \widehat {OCD} + \widehat {OCB} = \widehat {OBC} + \widehat {OBA}\)

Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\).

Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.

CH

Trả lời câu hỏi Câu hỏi trang 85 SGK Toán 9 Kết nối tri thức

Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?

Phương pháp giải:

+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra

\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)

+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).

+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).

Lời giải chi tiết:

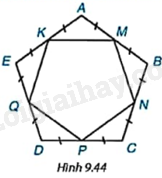
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).

Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).

Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)

Do đó,

+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)

+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)

Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.

Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)

Suy ra:

\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)

Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)

Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)

LT1

Trả lời câu hỏi Luyện tập 1 trang 86 SGK Toán 9 Kết nối tri thức

Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?

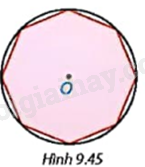
Phương pháp giải:

+ Chứng minh \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\) nên \(KM = MN = PN = PQ = QK\).

+ Chứng minh được \(\widehat {KMA} = \widehat {BMN}\) và \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o} \Rightarrow \widehat {KMN} = {180^o} - 2\widehat {KMA}\).

+ Chứng minh tương tự ta có: \(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\). Do đó, đa giác MNPQK là ngũ giác đều.

Lời giải chi tiết:

Vì ABCDE là ngũ giác đều nên \(AB = BC = CD = DE = EA\), \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)

Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA.

Do đó, \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\)

Ta có: \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\) và \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)

Suy ra: \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\)

Do đó: + \(KM = MN = PN = PQ = QK\left( 1 \right)\).

+ \(\widehat {KMA} = \widehat {AKM} = \widehat {BMN} = \widehat {MNB} = \widehat {CNP} = \widehat {CPN} = \widehat {DPQ} = \widehat {DQP} = \widehat {EQK} = \widehat {EKQ}\)

Ta có: \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o}\) (các góc kề bù)

Mà \(\widehat {KMA} = \widehat {BMN}\) nên \(\widehat {KMN} = {180^o} - 2\widehat {KMA}\).

Vì \(\widehat {BNM} + \widehat {MNP} + \widehat {PNC} = {180^o}\) (các góc kề bù)

Mà \(\widehat {KMA} = \widehat {BNM} = \widehat {PNC}\) nên \(\widehat {MNP} = {180^o} - 2\widehat {KMA}\).

Chứng minh tương tự ta có:

\(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\)

Do đó, \(\widehat {KMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQK} = \widehat {QKM}\left( 2 \right)\)

Từ (1) và (2) suy ra: MNPQK là ngũ giác đều.

TTN1

Trả lời câu hỏi Thử thách nhỏ 1 trang 87 SGK Toán 9 Kết nối tri thức

Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?

Phương pháp giải:

+ Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O). 

+ Chứng minh \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)

+ Tính được: \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)

+ Do đó \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\)

Lời giải chi tiết:

Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).

Vì ABCDEFGH là bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).

Vì ABCDEFGH là bát giác đều nội tiếp (O) nên \(OA = OB = OC = OD = OE = OF = OH = OG\).

Do đó, \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)

Suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)

Tam giác AOB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA}\).Do đó, \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)

Chứng minh tương tự ta có:

\(\widehat {OBC} = \widehat {OCB} = \widehat {ODE} = \widehat {OED} = \widehat {OEF} = \widehat {OFE} = \widehat {OFG} = \widehat {OGF} = \widehat {OGH} = \widehat {OHG} = \widehat {OHA} = \widehat {OAH} = 67,{5^o}\)

Suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\).

Vậy mỗi góc của bát giác đều bằng \({135^o}\).