Giải mục 1 trang 8, 9 SGK Toán 9 tập 1 - Cùng khám phá

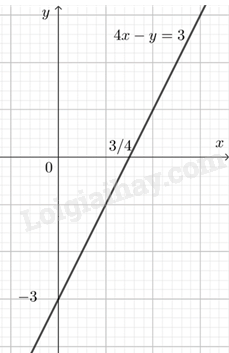
HĐ1

Trả lời câu hỏi Hoạt động 1 trang 8 SGK Toán 9 Cùng khám phá

a) Số tuổi của anh là $x$, số tuổi của em là $y$. Lập một hệ thức biểu diễn sự liên hệ giữa $x$ và $y$, biết anh lớn hơn em 5 tuổi.

b) 500 kg gạo được chia thành $x$ bao 50 kg và $y$ bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa $x$ và $y$.

Phương pháp giải:

Dựa vào các mối liên hệ giữa $x$ và $y$ để lập hệ thức.

Lời giải chi tiết:

a) Do anh lớn hơn em 5 tuổi nên ta có hệ thức biểu diễn sự liên hệ giữa $x$ và $y$ là: $x - y = 5$.

b) Do 500 kg gạo được chia thành $x$ bao 50 kg và $y$ bao 20 kg nên ta có hệ thức biểu diễn sự liên hệ giữa $x$ và $y$ là: $50x + 20y = 500$.

LT1

Trả lời câu hỏi Luyện tập 1 trang 8 SGK Toán 9 Cùng khám phá

Chỉ ra các phương trình bậc nhất hai ẩn $x$ và $y$ trong các phương trình sau:

$\begin{array}{l}5y - x =  - 2;\\3{x^2} - 10y = 1;\\\frac{{{x^2}}}{{x + 1}} - y = 0;\\x + 0y = 4;\\{y^2} - 9x =  - 6.\end{array}$

Phương pháp giải:

Dựa vào định nghĩa phương trình bậc nhất hai ẩn $x$ và $y$  để xác định.

Lời giải chi tiết:

Các phương trình bậc nhất hai ẩn $x$ và $y$ là: $5y - x =  - 2;\,\,x + 0y = 4$.

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 9 SGK Toán 9 Cùng khám phá

a) Cặp số $\left( {x_1^{};y_1^{}} \right) = \left( {8;5} \right)$ có thỏa mãn $50x_1^{} + 20y_1^{} = 500$ không?

b) Tìm một cặp số $\left( {x_2^{};y_2^{}} \right)$ khác cặp số $\left( {8;5} \right)$ sao cho $50x_2^{} + 20y_2^{} = 500$.

c) Tìm một cặp số $\left( {x_3^{};y_3^{}} \right)$ sao cho $50x_3^{} + 20y_3^{} \ne 500$.

Phương pháp giải:

a) Thay cặp số vào phương trình để kiểm tra.

b) Thay $x$ vào phương trình để tìm $y$ rồi xác định cặp số.

c) Cho một cặp số khác 2 cặp số vừa tìm được.

Lời giải chi tiết:

a) Vì $50.8 + 20.5 = 500$ nên cặp số $\left( {8;5} \right)$ thỏa mãn $50x_1^{} + 20y_1^{} = 500$.

b) Thay $y_2^{} = 10$ vào phương trình ta được:

$\begin{array}{l}50x_2^{} + 20.10 = 500\\50x_2^{} = 300\\x_2^{} = 6\end{array}$

Vậy cặp số $\left( {6;10} \right)$ là một cặp số thỏa mãn $50x_2^{} + 20y_2^{} = 500$.

c) Vì $50.8 + 20.3 \ne 500$ nên cặp số $\left( {8;3} \right)$ thỏa mãn $50x_3^{} + 20y_3^{} \ne 500$.

LT2

Trả lời câu hỏi Luyện tập 2 trang 9 SGK Toán 9 Cùng khám phá

Tìm bốn nghiệm của phương trình $3x - 4y = 5$.

Phương pháp giải:

Tìm cặp số thỏa mãn phương trình để kết luận nghiệm.

Lời giải chi tiết:

+ Vì $3.1 - 4.\frac{{ - 1}}{2} = 5$ nên cặp số $\left( {1; - \frac{1}{2}} \right)$ là một nghiệm của phương trình $3x - 4y = 5$.

+ Vì $3.2 - 4.\frac{1}{4} = 5$ nên cặp số $\left( {2;\frac{1}{4}} \right)$ là một nghiệm của phương trình $3x - 4y = 5$.

+ Vì $3.3 - 4.1 = 5$ nên cặp số $\left( {3;1} \right)$ là một nghiệm của phương trình $3x - 4y = 5$.

+ Vì $3.4 - 4.\frac{7}{4} = 5$ nên cặp số $\left( {4;\frac{7}{4}} \right)$ là một nghiệm của phương trình $3x - 4y = 5$.

LT3

Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 9 Cùng khám phá

Trong mặt phẳng tọa độ $Oxy$, hãy biểu diễn các nghiệm của mỗi phương trình sau:

a) $4x - y = 3$

b) $0x - 2y = 5$

c) $7x + 0y = 21$

Phương pháp giải:

+ Biểu diễn $x$ theo $y$ hoặc $y$ theo $x$.

+ Tìm hai cặp số là nghiệm của phương trình.

+ Vẽ đồ thị.

Lời giải chi tiết:

a) Xét phương trình $4x - y = 3$.      (1)

Chuyển vế, ta có $y = 4x - 3$.

Nếu cho $x$ một giá trị bất kì thì cặp số $\left( {x;y} \right)$, trong đó $y = 4x - 3$, là một nghiệm của phương trình (1) có các nghiệm là $\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4x - 3.\end{array} \right.$

Trong mặt phẳng tọa độ $Oxy$, tập hợp các điểm biểu diễn các nghiệm của phương trình (1) là đường thẳng $y = 4x - 3$.

b) Xét phương trình $0x - 2y = 5$.      (2)

Từ (2), ta có $2y = 5$ hay $y = \frac{5}{2}$.

Nếu cho $x$ một giá trị bất kì thì cặp số $\left( {x;y} \right)$, trong đó $y = \frac{5}{2}$, là một nghiệm của phương trình (2).

Do đó phương trình (2) có các nghiệm là $\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{5}{2}.\end{array} \right.$

Trong mặt phẳng tọa độ $Oxy$, tập hợp các điểm biểu diễn các nghiệm của phương trình (2) là đường thẳng đi qua điểm $A\left( {0;\frac{5}{2}} \right)$ và song song với trục hoành (ta gọi đường thẳng này là đường thẳng $y = \frac{5}{2}$).

c) Xét phương trình $7x + 0y = 21$.        (3)

Từ (3), ta có $7x = 21$ hay $x = 3$.

Nếu cho $y$ một giá trị bất kì thì cặp số $\left( {x;y} \right)$, tron đó $x = 3$, là một nghiệm của phương trình (3).

Do đó phương trình (3) có các nghiệm là: $\left\{ \begin{array}{l}x = 3\\y \in \mathbb{R}.\end{array} \right.$

Trong mặt phẳng tọa độ $Oxy$, tập hợp các điểm biểu diễn các nghiệm của phương trình (3) là đường thẳng đi qua điểm $B\left( { - 3;0} \right)$ và song song với trục tung (ta gọi đường thẳng này là đường thẳng $x = 3$).