Giải mục 1 trang 75, 76, 77 SGK Toán 9 tập 2 - Chân trời sáng tạoCó nhận xét gì về các cạnh và góc của mỗi đa giác sau?
Lựa chọn câu để xem lời giải nhanh hơn
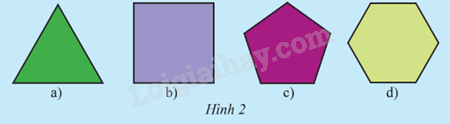
HĐ1 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Chân trời sáng tạo Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
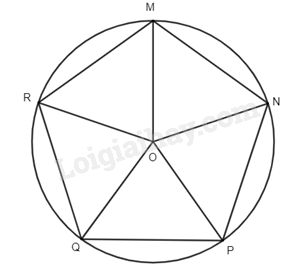
Phương pháp giải: Nhìn hình nhận xét. Lời giải chi tiết: - Độ dài các cạnh của mỗi đa giác là bằng nhau. - Số đo góc của mỗi đa giác là bằng nhau. TH1 Video hướng dẫn giải Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 9 Chân trời sáng tạo Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung ⌢MN,⌢NP,⌢PQ,⌢QR,⌢RM⌢MN,⌢NP,⌢PQ,⌢QR,⌢RM bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao? Phương pháp giải: - Đọc kĩ dữ kiện đề bài để vẽ hình - Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều. Lời giải chi tiết:
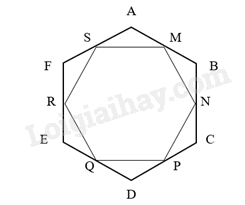
Các cung ⌢MN,⌢NP,⌢PQ,⌢QR,⌢RM⌢MN,⌢NP,⌢PQ,⌢QR,⌢RM chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360o : 5 = 72o. Ta có ^MONˆMON là góc nội tiếp chắn cung MN suy ra ^MONˆMON = 72o . Xét ΔΔMON, có: OM = ON = R suy ra ΔΔ MON cân tại O. Suy ra ^OMN=^ONMˆOMN=ˆONM (tính chất tam giác cân) Suy ra ^OMN=^ONM=180o−^MON2=54oˆOMN=ˆONM=180o−ˆMON2=54o. Tương tự, ta có ^OPN=^ONP=54oˆOPN=ˆONP=54o. Suy ra ^MPN=^ONM+^ONP=54o+54o=108oˆMPN=ˆONM+ˆONP=54o+54o=108o. Xét ΔΔ OMN và ΔΔ ONP có: ^MON=^NOPˆMON=ˆNOP; OM = OP; ON chung. Suy ra ΔΔ OMN = ΔΔ ONP (c – g – c). Do đó, MN = NP (hai cạnh tương ứng). Chứng minh tương tự ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau ( = 108o). Vậy MNPQR là một đa giác đều. VD1 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 1 trang 77 SGK Toán 9 Chân trời sáng tạo Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao? Phương pháp giải: - Đọc kĩ dữ kiện đề bài để vẽ hình - Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều. Lời giải chi tiết:
Do ABCDEF là lục giác đều nên: ˆA=ˆB=ˆC=ˆD=ˆE=ˆF=120oˆA=ˆB=ˆC=ˆD=ˆE=ˆF=120o. - AB = BC = CD = DE = EF = FA. Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA. Xét ΔΔ SAM và ΔΔ MBN có: ˆA=ˆBˆA=ˆB (chứng minh trên); AM = BN (chứng minh trên); SA = MB (chứng minh trên). Suy ra ΔΔ SAM = ΔΔ MBN (c – g – c). Do đó, SM = MN (hai cạnh tương ứng). Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM (1). Vì AS = AM (chứng minh trên) suy ra ΔΔ ASM cân tại A. suy ra ^ASM=^AMSˆASM=ˆAMS (tính chất tam giác cân) Nên ^ASM=^AMS=180o−ˆA2=30oˆASM=ˆAMS=180o−ˆA2=30o (tổng 3 góc trong của tam giác). Tương tự ta thu được: ^BMN=^BNM=180o−ˆB2=30ˆBMN=ˆBNM=180o−ˆB2=30; ^CNP=^CPN=180o−ˆC2=30oˆCNP=ˆCPN=180o−ˆC2=30o; ^DPQ=^DQP=180o−ˆD2=30oˆDPQ=ˆDQP=180o−ˆD2=30o; ^EQR=^ERQ=180o−ˆE2=30oˆEQR=ˆERQ=180o−ˆE2=30o;. ^FRS=^FSR=180o−ˆF2=30o Ta có: ^RSM=180o−^FRS−^ASM=180o−30o−30o=120o Tương tự, ta được: ^AMN=^MNP=^NQP=^PQR=^QRS=120o. (2) Từ (1) và (2), suy ra MNPQRS là đa giác đều.
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|