Giải mục 1 trang 74, 75, 76 SGK Toán 12 tập 1 - Cùng khám pháTrong không gian Oxyz, cho hai vectơ (vec a = ({x_1};{y_1};{z_1})) và (vec b = ({x_2};{y_2};{z_2})). a) Hãy biểu diễn các vectơ (vec a), (vec b) theo ba vectơ đơn vị (vec i), (vec j), (vec k). b) Tính (vec a + vec b) theo (vec i), (vec j), (vec k), từ đó tìm tọa độ của vectơ (vec a + vec b).
Lựa chọn câu để xem lời giải nhanh hơn
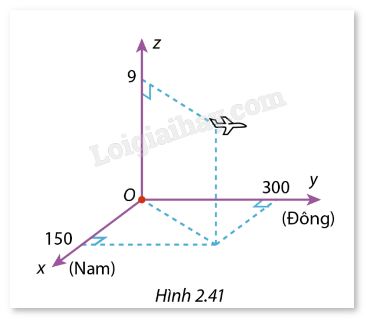
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 74 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho hai vectơ →a=(x1;y1;z1) và →b=(x2;y2;z2). a) Hãy biểu diễn các vectơ →a, →b theo ba vectơ đơn vị →i, →j, →k. b) Tính →a+→b theo →i, →j, →k, từ đó tìm tọa độ của vectơ →a+→b. Phương pháp giải: - Mỗi vectơ trong không gian Oxyz với tọa độ (x,y,z) có thể được biểu diễn dưới dạng: →v=x→i+y→j+z→k - Cộng các thành phần tương ứng của hai vectơ để tìm tổng: →a+→b=(x1+x2)→i+(y1+y2)→j+(z1+z2)→k Lời giải chi tiết: a) Vectơ →a có tọa độ (x1,y1,z1) nên nó có thể được biểu diễn theo các vectơ đơn vị →i,→j,→k như sau: →a=x1→i+y1→j+z1→k Tương tự, vectơ →b có tọa độ (x2,y2,z2) nên: →b=x2→i+y2→j+z2→k b) Tổng của hai vectơ →a+→b là: →a+→b=(x1→i+y1→j+z1→k)+(x2→i+y2→j+z2→k) Kết hợp các thành phần tương ứng: →a+→b=(x1+x2)→i+(y1+y2)→j+(z1+z2)→k Vậy tọa độ của vectơ →a+→b là (x1+x2;y1+y2;z1+z2). LT1 Trả lời câu hỏi Luyện tập 1 trang 75 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho ba điểm A(5; -3; 0), B(2; 1; -1), C(4; 1; 2). a) Tìm tọa độ của vectơ →u=2→AB+→AC−5→BC. b) Tìm điểm N sao cho 2→NA=−→NB Phương pháp giải: a) Tính toạ độ của các vectơ →AB,→AC và →BC sau đó thay vào biểu thức để xác định toạ độ của →u. b) - Gọi toạ độ của N là (x,y,z). - Biểu diễn →NA,→NB theo x, y, z. - Sử dụng điều kiện 2→NA=−→NB để thiết lập hệ phương trình. - Giải hệ phương trình để tìm toạ độ N. Lời giải chi tiết: a) Trước hết, chúng ta tính các vectơ →AB, →AC, và →BC: →AB=→B−→A=(2−5;1+3;−1−0)=(−3;4;−1) →AC=→C−→A=(4−5;1+3;2−0)=(−1;4;2) →BC=→C−→B=(4−2;1−1;2+1)=(2;0;3) Bây giờ tính vectơ →u: →u=2→AB+→AC−5→BC Thay các vectơ đã tính: →u=2(−3;4;−1)+(−1;4;2)−5(2;0;3) →u=(−6;8;−2)+(−1;4;2)−(10;0;15) →u=(−6−1−10;8+4−0;−2+2−15) →u=(−17;12;−15) Vậy tọa độ của vectơ →u là (−17;12;−15). b) Điều kiện 2→NA=−→NB có thể được viết lại như sau: 2(→A−→N)=(→B−→N) Giải phương trình này: 2→A−2→N=−→B+→N Chuyển vế: 3→N=2→A+→B Từ đó: →N=2→A+→B3 Tính tọa độ của điểm N: →N=2(5;−3;0)+(2;1;−1)3 →N=(10;−6;0)+(2;1;−1)3=(12;−5;−1)3 →N=(4;−53;−13) Vậy tọa độ của điểm N là (4;−53;−13). LT2 Trả lời câu hỏi Luyện tập 2 trang 75 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho ba điểm A(4; 1; -1), B(2; -1; 5), C(3; 0; 2). Chứng minh rằng ba điểm A, B, C thẳng hàng. Phương pháp giải: Ba điểm A, B, C thẳng hàng khi và chỉ khi vectơ →AB và →AC cùng phương. Lời giải chi tiết: Tính các vectơ →AB và →AC: →AB=→B−→A=(2−4;−1−1;5+1)=(−2;−2;6) →AC=→C−→A=(3−4;0−1;2+1)=(−1;−1;3) Xét tỉ lệ: −2−1=2,−2−1=2,63=2 Vì →AB→AC=2, hai vectơ này cùng phương, nên ba điểm A, B, C thẳng hàng. VD1 Trả lời câu hỏi Vận dụng 1 trang 75 SGK Toán 12 Cùng khám phá Trong Hình 2.41, gốc tọa độ O là nơi máy bay xuất phát, trục Ox theo hướng Nam, trục Oy theo hướng Đông, trục Oz theo hướng thẳng đứng. Đơn vị trên các trục là km. Vào thời điểm 9h30 sáng, máy bay ở độ cao 9 km, cách điểm xuất phát theo hướng Nam 150 km và theo hướng Đông 300 km. Phi công để chế độ bay tự động, với vận tốc theo hướng Đông 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng Bắc với vận tốc 10 m/s. Tìm tọa độ của máy bay lúc 10h30, với giả định là trong khoảng thời gian 9h30 đến 10h30, vận tốc và hướng của gió không thay đổi.
Phương pháp giải: - Tìm tọa độ của máy bay tại thời điểm ban đầu. - Tính vận tốc của máy bay theo các trục Ox, Oy (bao gồm cả ảnh hưởng của gió) và xác định vận tốc theo trục Oz. - Sử dụng công thức x=x0+vx×t, y=y0+vy×t, z=z0+vz×t để tính tọa độ máy bay sau thời gian t. Lời giải chi tiết: Tọa độ máy bay lúc 9h30 là: A = (150; 300; 9). Vận tốc gió là 10 m/s = 36 km/h. Hướng di chuyển của máy bay trong 1 giờ là: →v=(−36;750;0). Tọa độ của máy bay lúc 10h30 là: B = (150 – 36; 300 + 750; 9 + 0) = (114; 1050; 9). HĐ2 Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, tam giác ABC có A(xA,yA,zA), B(xB,yB,zB), và C(xC,yC,zC) a) Gọi M là trung điểm của đoạn thẳng A B. Tìm tọa độ điểm M. b) Gọi G là trọng tâm tam giác ABC. Tìm tọa độ điểm G. Phương pháp giải: - Công thức trung điểm: Tọa độ trung điểm M của đoạn thẳng nối hai điểm A(xA,yA,zA) và B(xB,yB,zB) được tính theo công thức: M(xA+xB2,yA+yB2,zA+zB2) - Công thức trọng tâm: Tọa độ trọng tâm G của tam giác có các đỉnh A(xA,yA,zA),B(xB,yB,zB), và C(xC,yC,zC) được tính theo công thức: G(xA+xB+xC3,yA+yB+yC3,zA+zB+zC3) Lời giải chi tiết: a) Tọa độ điểm M là: M(xA+xB2,yA+yB2,zA+zB2) b) Tọa độ điểm G là: G(xA+xB+xC3,yA+yB+yC3,zA+zB+zC3) LT3 Trả lời câu hỏi Luyện tập 3 trang 76 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho ba điểm A(1;3;−5), M(32;2;−12), G(2;23;−23). a) Tìm tọa độ điểm B sao cho M là trung điểm của đoạn thẳng AB. b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC. Phương pháp giải: - Tọa độ điểm B: Sử dụng công thức trung điểm: xB=2xM−xA,yB=2yM−yA,zB=2zM−zA. Thay tọa độ A và M để tìm B. - Tọa độ điểm C: Sử dụng công thức trọng tâm: xC=3xG−(xA+xB),yC=3yG−(yA+yB),zC=3zG−(zA+zB). Thay tọa độ A, B, và G để tìm C. Lời giải chi tiết: a) Ta có tọa độ điểm M là trung điểm của AB nên: M(xA+xB2,yA+yB2,zA+zB2) Từ đó, tọa độ điểm B được xác định bằng cách giải phương trình: xB=2xM−xA,yB=2yM−yA,zB=2zM−zA Thay toạ độ của điểm A, M vào: xB=2×32−1=2,yB=2×2−3=1,zB=2×(−12)−(−5)=4 Vậy tọa độ điểm B là B(2; 1; 4). b) Vì G là trọng tâm của tam giác ABC, ta có: G(xA+xB+xC3,yA+yB+yC3,zA+zB+zC3) Từ đó, ta có hệ phương trình: xC=3xG−(xA+xB),yC=3yG−(yA+yB),zC=3zG−(zA+zB) Thay toạ độ của điểm A, B, G vào: xC=3×2−(1+2)=3,yC=3×23−(3+1)=0,zC=3×(−23)−(−5+4)=−3 Vậy tọa độ điểm C là C (3; 0; -3).
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|