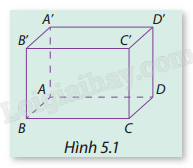
Giải mục 1 trang 41, 42, 43 SGK Toán 12 tập 2 - Cùng khám pháXét các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp chữ nhật ABCD.A′B′C′D′ (Hình 5.1). a) Tìm bốn vectơ có giá trị vuông góc với mặt phẳng (ABCD). b) Tìm hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng (ABCD).
Lựa chọn câu để xem lời giải nhanh hơn
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 41 SGK Toán 12 Cùng khám phá Xét các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp chữ nhật ABCD.A′B′C′D′ (Hình 5.1). a) Tìm bốn vectơ có giá trị vuông góc với mặt phẳng (ABCD). b) Tìm hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng (ABCD).
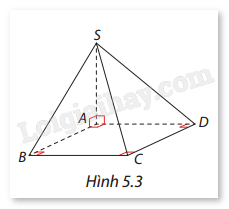
Phương pháp giải: - Để tìm các vectơ vuông góc với mặt phẳng (ABCD), ta tìm các vectơ có phương vuông góc với các vectơ nằm trong mặt phẳng này. - Để tìm các vectơ nằm trong mặt phẳng (ABCD), ta xét các vectơ có giá là các đoạn thẳng trong mặt phẳng đó hoặc song song với nó. Lời giải chi tiết: a) - Các vectơ vuông góc với mặt phẳng (ABCD) sẽ có phương vuông góc với mặt phẳng này. Các vectơ này sẽ có phương dọc theo trụcAA′,BB′,CC′,DD′, vì các đoạn thẳng nối đỉnh giữa hai mặt phẳng song song (ABCD) và (A′B′C′D′) đều vuông góc với mặt phẳng (ABCD). - Các vectơ cần tìm là: →AA′,→BB′,→CC′,→DD′ Đây là các vectơ có giá trị vuông góc với mặt phẳng (ABCD), vì chúng có phương dọc theo chiều cao của hình hộp chữ nhật, vuông góc với mặt phẳng đáy (ABCD). b) - Các vectơ nằm trong mặt phẳng (ABCD) có phương song song với các cạnh của hình chữ nhậtABCD. - Hai vectơ không cùng phương có thể lấy như sau: →AB,→AC Đây là các vectơ có giá nằm trong mặt phẳng (ABCD), lần lượt dọc theo hai cạnh của hình chữ nhậtABCD. LT1 Trả lời câu hỏi Luyện tập 1 trang 42 SGK Toán 12 Cùng khám phá Cho hình chóp S.ABCD với ABCD là hình vuông và SA vuông góc với (ABCD). a) Tìm một vectơ pháp tuyến của các mặt phẳng (ABCD), (SAB), (SAD), và (SAC). b) Tìm hai cặp vectơ chỉ phương của mặt phẳng (SCD).
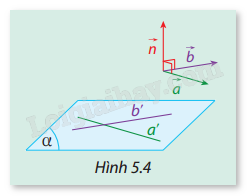
Phương pháp giải: - Vectơ pháp tuyến của một mặt phẳng là một vectơ vuông góc với tất cả các vectơ thuộc mặt phẳng đó. - Hai vectơ chỉ phương của một mặt phẳng là hai vectơ không đồng phương và cùng nằm trong mặt phẳng đó. Lời giải chi tiết: a) - Mặt phẳng (ABCD): Theo đề bài, ta có SA vuông với mặt phẳng (ABCD) nên →SA cũng là vectơ pháp tuyến của mặt phẳng (ABCD). - Mặt phẳng (SAB): Ta chọn các vectơ chỉ phương: →SA,→AB Theo đề bài, ta có DA vuông góc với →SA,→AB nên →DA là một vectơ pháp tuyến của mặt phẳng (SAB). - Mặt phẳng (SAD): Chọn các vectơ chỉ phương: →SA,→AD Theo đề bài, ta có BA vuông góc với →SA,→AD nên →BA là một vectơ pháp tuyến của mặt phẳng (SAD). - Mặt phẳng (SAC): Chọn các vectơ chỉ phương: →SA,→AC Theo đề bài, ta có BD vuông góc với →SA,→AC nên →BD là một vectơ pháp tuyến của mặt phẳng (SAC). b) Các vectơ chỉ phương của mặt phẳng này là: →SC,→CD và →SD,→DC HĐ2 Trả lời câu hỏi Hoạt động 2 trang 42 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho mặt phẳng (α) có cặp vectơ chỉ phương →a=(a1,a2,a3) và →b=(b1,b2,b3) (Hình 5.4). Xét vectơ →n được xác định như sau: →n=(a2b3−a3b2,a3b1−a1b3,a1b2−a2b1) Tính →n⋅→a và →n⋅→b. Vectơ →n có phải là một vectơ pháp tuyến của mặt phẳng (α) không? Vì sao?
Phương pháp giải: Giả sử hai vectơ →a và →b có tọa độ lần lượt là: →a=(a1,a2,a3),→b=(b1,b2,b3) Công thức tích vô hướng của chúng là: →a⋅→b=a1b1+a2b2+a3b3 Lời giải chi tiết: - Tính tích vô hướng →n⋅→a: Ta có: →n⋅→a=(a2b3−a3b2)a1+(a3b1−a1b3)a2+(a1b2−a2b1)a3 Sau khi phân tích và đơn giản hóa, kết quả sẽ là 0. - Tính tích vô hướng →n⋅→b: Tương tự: →n⋅→b=(a2b3−a3b2)b1+(a3b1−a1b3)b2+(a1b2−a2b1)b3 Sau khi tính toán, kết quả cũng là 0. Vì →n⋅→a=0 và →n⋅→b=0, vectơ →n vuông góc với cả →a và →b. Do đó, →n là vectơ pháp tuyến của mặt phẳng (α). LT2 Trả lời câu hỏi Luyện tập 2 trang 43 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho tứ diện ABCD có các đỉnh là A(5;1;3), B(1;6;2), C(5;0;4) và D(4;0;6). Tìm một vectơ pháp tuyến của mặt phẳng (α) chứa cạnh AB và song song với cạnh CD. Phương pháp giải: Vì mặt phẳng (α) chứa cạnh AB và song song với cạnh CD, nên vectơ pháp tuyến của mặt phẳng (α) sẽ vuông góc với cả →AB và →CD. Vectơ pháp tuyến của mặt phẳng (α) là tích có hướng của hai vectơ: →n=→AB×→CD. Lời giải chi tiết: Tính vectơ chỉ phương của các cạnh: →AB=B−A=(1−5,6−1,2−3)=(−4,5,−1) →CD=D−C=(4−5,0−0,6−4)=(−1,0,2) Tính tích có hướng →n=→AB×→CD: →n=|ijk−45−1−102| Tính từng bước: →n=i|5−102|−j|−4−1−12|+k|−45−10| =i(5⋅2−(−1)⋅0)−j(−4⋅2−(−1)⋅(−1))+k(−4⋅0−5⋅(−1)) =i(10)−j(−8−1)+k(5) =(10,9,5) Vậy vectơ pháp tuyến của mặt phẳng (α) là: →n=(10,9,5)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|