Giải mục 1 trang 10,11,12 SGK Toán 12 tập 1 - Cùng khám phá

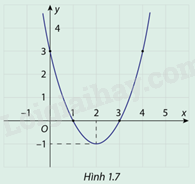
HĐ1

Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá

Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7

a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho

b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất

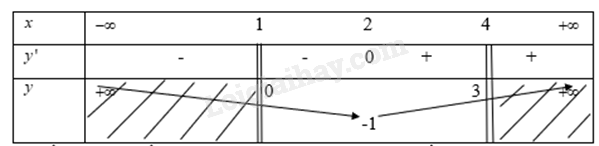
Phương pháp giải:

a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất

b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất

Lời giải chi tiết:

a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)

b) Ta có: \(y' = 2x - 4\)

Xét \(y' = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)

Ta có bảng biến thiên

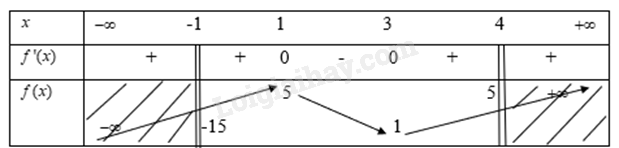
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất

LT1

Trả lời câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá

Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)

Phương pháp giải:

Bước 1: Tính\(f'(x)\)

Bước 2: Lập bảng biến thiên

Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)

Lời giải chi tiết:

Ta có: \(f'(x) = 3{x^2} - 12x + 9\)

Xét \(f'(x) = 0\)

 \( \Rightarrow 3{x^2} - 12x + 9 = 0\)

 \( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)

Ta có bảng biến thiên là

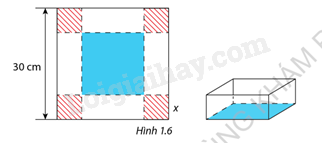
Từ bảng biến thiên ta thấy

Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)

Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x =  - 1\) khi đó \(y =  - 15\)

LT2

Trả lời câu hỏi Luyện tập 2 trang 12 SGK Toán 12 Cùng khám phá

Trong một trò chơi, mỗi đội được phát một tấm bìa hình vuông có cạnh bằng 30 cm. Nhiệm vụ của mỗi đội chơi là cắt ở 4 góc của tấm bìa này 4 hình vuông bằng nhau rồi gập tấm bìa lại( hình 1.6) và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật. Đội nào thiết kế được cái hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của các hình vuông bị cắt để thu được hộp có thể tích lớn nhất.

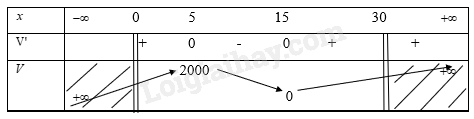
Phương pháp giải:

Bước 1: Lập công thức tính thể tích hình hộp dước dạng hàm số

Bước 2: Lập bảng biến thiên của hàm số

Bước 3: Tính thể tích lớn nhất của hình hộp là tìm giá trị lớn nhât của hàm số

Lời giải chi tiết:

Gọi độ dài hình vuông cần cắt là \(x(cm,0 < x < 30)\)

Khi đó độ dài cạnh hình hộp là\(30 - 2x\)(>0)

Thể tích hình hộp là

\(V = x(30 - 2x)(30 - 2x)\)

\( = 4{x^3} - 120{x^2} + 900x\)

Ta có \(V' = 12{x^2} - 240x + 900\)

Xét \(V' = 0\)

\( \Rightarrow 12{x^2} - 240x + 900 = 0\)

\( \Rightarrow \left[ \begin{array}{l}x = 5\\x = 15\end{array} \right.\)

Ta có bảng biến thiên

Từ bảng biến thiên ta thấy với \(x = 5\) thì thể tích hình hộp đạt giá trị lớn nhất là 2000