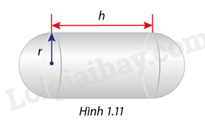
Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám pháMột thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0)và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000cho 1 \({m^2}\) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không đư Đề bài Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0) và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000 cho 1 \({m^2}\) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không được vượt quá 50m.
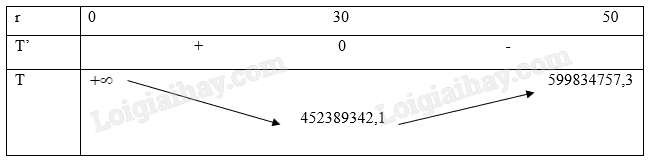
Phương pháp giải - Xem chi tiết Bước 1: Lập công thức tính chi phí sơn Bước 2: Lập bảng biến thiên của hàm số Bước 3: Tính chi phí nhỏ nhất để sơn là tìm giá trị bé nhấ tcủa hàm số Lời giải chi tiết Thể tích thùng chứa là \({V_{thung}} = {V_{tru}} + {V_{ca u}}\) \( = \pi {r^2}h + \frac{4}{3}\pi {r^3} = 144000\pi \) \( \Rightarrow 3{r^2}h + 4{r^3} = 432000\) \( \Rightarrow h = \frac{{432000 - 4{r^3}}}{{{r^2}}}\) Chi phí để sơn thùng chứa là \(P = 2\pi rh.10000 + 4\pi {r^2}.20000\) \( = 20000\pi (rh + 4{r^2})\)  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
