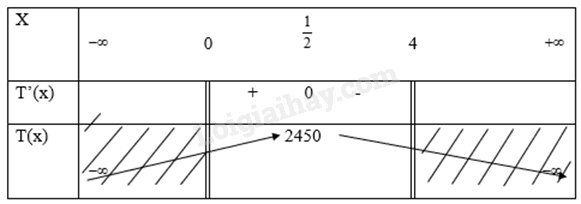
Giải bài tập 1.13 trang 14 SGK Toán 12 tập 1 - Cùng khám pháMột doạnh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện tại doạnh nghiệp đang tập trung vào chiến lược kinh doanh xe X với chi phi mua vào 27 triệu dộng và bán ra với giá 31 triệu đồng. với giá bán này, số lượng xe khách hàng đã mua trong 1 năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang bán chạy này, doanh nghiệp dự định sẽ giảm giá bán. Bộ phận nghiên cứu rằng nếu giảm 1 triệu đồng mỗi chiếu xe thì trong một năm số lượng xe bán ra trong một năm tăng Đề bài Một doạnh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện tại doạnh nghiệp đang tập trung vào chiến lược kinh doanh xe X với chi phi mua vào 27 triệu dộng và bán ra với giá 31 triệu đồng. với giá bán này, số lượng xe khách hàng đã mua trong 1 năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang bán chạy này, doanh nghiệp dự định sẽ giảm giá bán. Bộ phận nghiên cứu rằng nếu giảm 1 triệu đồng mỗi chiếu xe thì trong một năm số lượng xe bán ra trong một năm tăng thêm 200 chiếc. Hỏi theo đó, giá bán mới là bao nhiêu thì lợi nhuận thu được cao nhất? Phương pháp giải - Xem chi tiết Bước 1: Lập công thức tính lợi nhuận dưới dạng hàm số Bước 2: Lập bảng biến thiên của hàm số Bước 3: Tính lợi nhuận cao nhất là tìm gía trị lớn nhất của hàm số Lời giải chi tiết Gọi giá tiền giảm của mỗi chiếc xe là x ( triệu đồng, x<4) Khi đó lợi nhuận hằng năm thu được là T(x) = (31-27-x)(600+200x) \({\rm{ = - 200}}{{\rm{x}}^{\rm{2}}}{\rm{ + 200x + 2400}}\) \({\rm{T'(x) = - 400x + 200}}\) Xét \({\rm{T'(x) = 0}}\)\( \Rightarrow {\rm{x = }}\frac{{\rm{1}}}{{\rm{2}}}\) Ta có bảng biến thiên là
Vậy nếu giảm giá tiền mỗi chiếc xe \(\frac{{\rm{1}}}{{\rm{2}}}\) triệu đồng thì đạt doanh thu lớn nhất là 2450 triệu đồng  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
