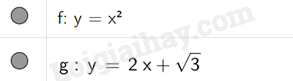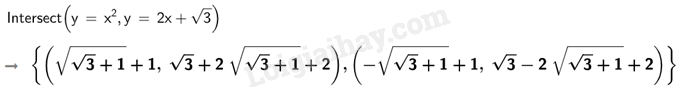Giải câu hỏi trang 114 SGK Toán 9 tập 2 - Kết nối tri thứcSử dụng phần mềm GeoGebra thực hiện các yêu cầu sau: Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Lựa chọn câu để xem lời giải nhanh hơn
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau: TH1 Video hướng dẫn giải Trả lời câu hỏi Thực hành 1 trang 114 SGK Toán 9 Kết nối tri thức Giải các phương trình sau: a) x2−4x+10=0x2−4x+10=0; b) x+9x−1=7x+9x−1=7; c) x2−2(√3−1)x−2√3=0x2−2(√3−1)x−2√3=0; d) x+1x−1−x−1x+1=4x2−1x+1x−1−x−1x+1=4x2−1. Phương pháp giải: + Để giải phương trình nói chung, ta dùng lệnh Solve (<phương trình>) hoặc Solutions (<phương trình>) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới. + Nghiệm của phương trình được biểu diễn dưới dạng tập hợp. Chú ý, kí hiệu {} thể hiện phương trình vô nghiệm. Lời giải chi tiết: a)
Vậy phương trình x2−4x+10=0x2−4x+10=0 vô nghiệm. b)
Vậy phương trình x+9x−1=7x+9x−1=7 có nghiệm x=4x=4. c)
Vậy phương trình x2−2(√3−1)x−2√3=0x2−2(√3−1)x−2√3=0 có nghiệm x=√3−3;x=√3+1x=√3−3;x=√3+1. d)
Vậy phương trình x+1x−1−x−1x+1=4x2−1x+1x−1−x−1x+1=4x2−1 vô nghiệm. TH2 Video hướng dẫn giải Trả lời câu hỏi Thực hành 2 trang 114 SGK Toán 9 Kết nối tri thức Giải các hệ phương trình sau: a) {3x−2y=42x+y=5; b) {x+y=53x+3√3y=6; c) {3x+2y=02x−3y=0; d) {x√5−(1+√3)y=1(1−√3)x+y√5=1. Phương pháp giải: Cách 1: Sử dụng câu lệnh Solve ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) hoặc Solutions ({<phương trình thứ nhất>, (<phương trình thứ hai>}, {<biến số thứ nhất>, (<biến số thứ hai>}) trên ô lệnh của cửa sổ CAS kết quả sẽ hiển thị ngay bên dưới. Cách 2: Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng. Lời giải chi tiết: a)
Vậy hệ phương trình {3x−2y=42x+y=5 có nghiệm x=2;y=1. b)
Vậy hệ phương trình {x+y=53x+3√3y=6 có nghiệm x=−33√32−93√3+138;y=33√32+93√3+278. c)
Vậy hệ phương trình {3x+2y=02x−3y=0 có nghiệm x=0;y=0. d)
Vậy hệ phương trình {x√5−(1+√3)y=1(1−√3)x+y√5=1 có nghiệm x=√53+√33+13;y=√53+√33−13. TH3 Video hướng dẫn giải Trả lời câu hỏi Thực hành 3 trang 114 SGK Toán 9 Kết nối tri thức Cho đường thẳng (d):y=2x+√3 và parabol (P):y=x2. a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của (d) và (P). Phương pháp giải: - Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số y=ax2(a≠0) và hàm số bậc nhất y=ax+b(a≠0) + Nhập công thức hàm số y=ax2 và y=ax+b vào từng ô lệnh trong cửa sổ CAS. + Nháy chuột chọn nút - Sử dụng câu lệnh Intersect ({<phương trình thứ nhất>, (<phương trình thứ hai>}) trên ô lệnh của cửa sổ CAS để tìm tọa độ giao điểm của hai đường thẳng có phương trình tương ứng. Lời giải chi tiết: a) Nhập
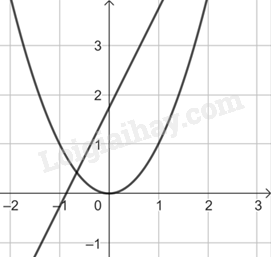
Ta được đồ thị
b)
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|













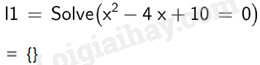
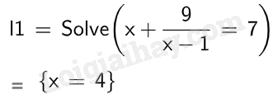
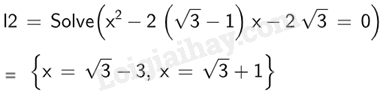
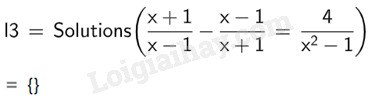
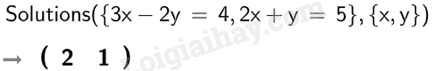
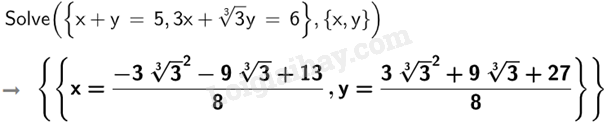
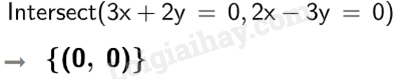
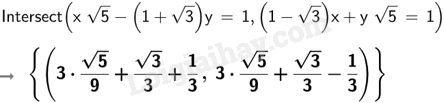
 ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.