Giải câu hỏi trắc nghiệm trang 17, 18 sách bài tập toán 9 - Kết nối tri thức tập 1Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn? A. (left{ begin{array}{l}2x + y = 3x - z = - 1end{array} right.). B. (left{ begin{array}{l}2x + y = 3�x + 0y = 1end{array} right.). C. (left{ begin{array}{l}2x + y = 3�x - y = - 1end{array} right.). D. (left{ begin{array}{l}2x + y = 3x + {y^2} = 1end{array} right.). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh
Lựa chọn câu để xem lời giải nhanh hơn
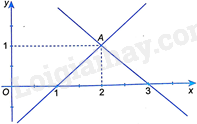
Câu 1 Trả lời câu hỏi Câu 1 trang 17 SBT Toán 9 Kết nối tri thức Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn? A. \(\left\{ \begin{array}{l}2x + y = 3\\x - z = - 1\end{array} \right.\). B. \(\left\{ \begin{array}{l}2x + y = 3\\0x + 0y = 1\end{array} \right.\). C. \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\). D. \(\left\{ \begin{array}{l}2x + y = 3\\x + {y^2} = 1\end{array} \right.\). Phương pháp giải: Một cặp gồm hai phương trình bậc nhất hai ẩn \(ax + by = c\) và \(a'x + b'y = c'\) được gọi là một hệ phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*). Lời giải chi tiết: Hệ \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\) là hệ hai phương trình bậc nhất hai ẩn. Chọn C Câu 2 Trả lời câu hỏi Câu 2 trang 17 SBT Toán 9 Kết nối tri thức Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là A. (-1; 1). B. (3; -1). C. \(\left( {\frac{1}{2}; - 1} \right)\). D. (2; -3). Phương pháp giải: Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình. Lời giải chi tiết: Sử dụng máy tính cầm tay, ta có nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là (2; -3). Chọn D Câu 3 Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 2), N(2; 3), P(-1; -1), Q(5; 8). Đường thẳng \(3x - 2y = - 1\) đi qua hai điểm nào trong các điểm đã cho? A. M và N. B. M và P. C. P và Q. D. N và P. Phương pháp giải: Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có: \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì đường thẳng \(ax + by = c\) đi qua điểm A\(\left( {{x_0};{y_0}} \right)\). Lời giải chi tiết: Với \(x = 1,y = 2\) ta có: \(3.1 - 2.2 = - 1\) nên điểm M(1; 2) thuộc đường thẳng \(3x - 2y = - 1\). Với \(x = 2,y = 3\) ta có: \(3.2 - 2.3 = 0 \ne - 1\) nên điểm N(2; 3) không thuộc đường thẳng \(3x - 2y = - 1\). Với \(x = - 1,y = - 1\) ta có: \(3.\left( { - 1} \right) - 2.\left( { - 1} \right) = - 1\) nên điểm P(-1; -1) thuộc đường thẳng \(3x - 2y = - 1\). Với \(x = 5,y = 8\) ta có: \(3.5 - 2.8 = - 1\) nên điểm Q(5; 8) thuộc đường thẳng \(3x - 2y = - 1\). Vậy đường thẳng \(3x - 2y = - 1\) đi qua các điểm M, P, Q. Chọn B, C Câu 4 Trả lời câu hỏi Câu 4 trang 18 SBT Toán 9 Kết nối tri thức Giá trị của a và b để đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) là A. \(a = 1,b = - 2\). B. \(a = - 5,b = 1\). C. \(a = - 3,b = 2\). D. \(a = - 1,b = 0\). Phương pháp giải: + Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\) + Giải hệ phương trình vừa tìm được bằng phương pháp cộng đại số ta tìm được a, b. Lời giải chi tiết: Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\) Cộng từng vế của hai phương trình trong hệ ta được: \(2b = 4\), suy ra \(b = 2\). Chọn C Câu 5 Trả lời câu hỏi Câu 5 trang 18 SBT Toán 9 Kết nối tri thức Hệ phương trình nào sau đây có nghiệm duy nhất? A. \(\left\{ \begin{array}{l}x - 2y = 3\\2x - 4y = 5\end{array} \right.\). B. \(\left\{ \begin{array}{l}x - 2y = 3\\ - 2x + 4y = - 6\end{array} \right.\). C. \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\). D. \(\left\{ \begin{array}{l}x - 2y = 3\\ - x + 2y = - 2\end{array} \right.\). Phương pháp giải: Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình. Lời giải chi tiết: Sử dụng máy tính cầm tay, ta thấy hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\) có nghiệm duy nhất là \(\left( {\frac{{11}}{4};\frac{{ - 1}}{8}} \right)\). Chọn C Câu 6 Trả lời câu hỏi Câu 6 trang 18 SBT Toán 9 Kết nối tri thức Hình bên dưới minh họa tập nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x - y = 1\\x - y = 3\end{array} \right.\). B. \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\). C. \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\). D. \(\left\{ \begin{array}{l}x + y = 1\\x + y = 3\end{array} \right.\). Phương pháp giải: + Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1). + Dùng máy tính cầm tay để tính, ta tìm hệ phương trình nào có nghiệm duy nhất là (2; 1) thì đó là hệ phương trình cần tìm. Lời giải chi tiết: Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1). Sử dụng máy tính bỏ túi, ta thấy chỉ có hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\) có nghiệm duy nhất là (2; 1). Chọn B Câu 7 Trả lời câu hỏi Câu 7 trang 18 SBT Toán 9 Kết nối tri thức Hệ phương trình \(\left\{ \begin{array}{l}3x - ay = b\\ax + by = 3\end{array} \right.\) có nghiệm là (2; -3) khi A. \(a = 3,b = 3\). B. \(a = 3,b = - 3\). C. \(a = - 3,b = 3\). D. \(a = - 3,b = - 3\). Phương pháp giải: + Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\) + Dùng máy tình cầm tay để tìm nghiệm của hệ phương trình thu được. Lời giải chi tiết: Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\) hay \(\left\{ \begin{array}{l} - 3a + b = 6\\2a - 3b = 3\end{array} \right.\) Sử dụng máy tính cầm tay, ta tìm được \(a = - 3;b = - 3\) Chọn D Câu 8 Trả lời câu hỏi Câu 8 trang 18 SBT Toán 9 Kết nối tri thức Hệ phương trình \(\left\{ \begin{array}{l}x + my = 1\\ - mx - y = - 1\end{array} \right.\) có vô số nghiệm trong trường hợp nào sau đây? A. \(m = 1\). B. \(m = - 1\). C. \(m = 2\). D. \(m = - 2\). Phương pháp giải: Thay từng giá trị của m trong từng đáp án, ta thu được hệ hai phương trình bậc nhất hai ẩn, giải phương hệ trình đó để tìm đáp án đúng. Lời giải chi tiết: Với \(m = 1\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1\\ - x - y = - 1\end{array} \right.\). Cộng từng vế của hai phương trình trong hệ ta có: \(0x + 0y = 0\). Hệ thức này đúng với mọi giá trị của x và y. Với giá trị tùy ý của y, giá trị của x được tính bằng \(x = 1 - y\). Vậy hệ phương trình đã cho có nghiệm là \(\left( {1 - y;y} \right)\) với \(y \in \mathbb{R}\) tùy ý khi \(m = 1\). Chọn A
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|