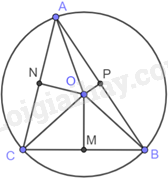
Giải bài tập 9.41 trang 92 SGK Toán 9 tập 2 - Kết nối tri thứcCho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp. Video hướng dẫn giải Phương pháp giải - Xem chi tiết + Chứng minh được OM⊥BC,ON⊥AC,OP⊥AB. + Chứng minh ΔANO vuông tại N và ΔAOP vuông tại P nên tứ giác ANOP là tứ giác nội tiếp. + Chứng minh ΔCNO vuông tại N và ΔCOM vuông tại M nên tứ giác CMON là tứ giác nội tiếp. + Chứng minh ΔMOB vuông tại M và ΔBOP vuông tại P nên tứ giác BPOM là tứ giác nội tiếp. Lời giải chi tiết
ΔAOB có OA=OB (bán kính đường tròn (O)) nên ΔOAB cân tại O, OP là đường trung tuyến đồng thời là đường cao. Suy ra: OP⊥AB nên ΔOPA vuông tại P và ΔOBP vuông tại P. Chứng minh tương tự ta có: ΔMOB vuông tại M, ΔCOM vuông tại M, ΔNOC vuông tại N, ΔNOA vuông tại N. Vì ΔOPA vuông tại P nên P thuộc đường tròn đường kính AO, ΔNOA vuông tại N nên N thuộc đường tròn đường kính AO. Do đó, tứ giác ANOP nội tiếp đường tròn đường kính AO. Vì ΔOPB vuông tại P nên P thuộc đường tròn đường kính BO, ΔMOB vuông tại M nên M thuộc đường tròn đường kính BO. Do đó, tứ giác BPOM nội tiếp đường tròn đường kính BO. Vì ΔCOM vuông tại M nên M thuộc đường tròn đường kính CO, ΔNOC vuông tại N nên N thuộc đường tròn đường kính CO. Do đó, tứ giác CMON nội tiếp đường tròn đường kính CO.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
