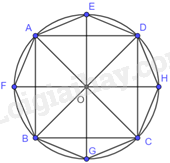
Giải bài tập 9.34 trang 91 SGK Toán 9 tập 2 - Kết nối tri thức

Đề bài

Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều ${45^o}$ biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?

Lời giải chi tiết

a) + Vẽ đường tròn (O). Trên đường tròn vẽ hình vuông ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.

+ Vẽ điểm E thuộc đường tròn (O) sao cho $\widehat {AOE} = {45^o}$ và tia OA quay thuận theo chiều kim đồng hồ đến tia OE.

+ Xác định các điểm F, G, H tương tự như xác định điểm E. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F, F với A ta được đa giác EAFBGCHD.

b) Vì A, E, D, H, C, G, B, F cùng thuộc (O) nên

$OA = OE = OD = OH = OC = OG = OB = OF$

Vì ABCD là hình vuông nên

$\widehat {AOD} = \widehat {DOC} = \widehat {BOC} = \widehat {BOA} = {90^o}$

Lại có: $\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = {45^o}$ nên $\widehat {DOE} = \widehat {AOF} = \widehat {BOG} = \widehat {COH} = {45^o}$

Ta có:

$\Delta AOE = \Delta DOE = \Delta DOH = \Delta COH = \Delta COG = \Delta BOG = \Delta BOF = \Delta AOF\left( {c.g.c} \right)$

Suy ra:

+) $AE = ED = DH = HC = CG = BG = BF = FA$

+) $\widehat {OAE} = \widehat {OEA} = \widehat {OED} = \widehat {ODE} = \widehat {ODH} = \widehat {OHD} = \widehat {OHC} = \widehat {OCH} = \widehat {OCG} = \widehat {OGC} = \widehat {OGB} = \widehat {OBG}$$= \widehat {OBF} = \widehat {OFB} = \widehat {OFA} = \widehat {FAO}$

Do đó, $\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}$

Đa giác EAFBGCHD có

$\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}$ và  $AE = ED = DH = HC = CG = BG = BF = FA$ nên đa giác EAFBGCHD là hình bát giác đều.