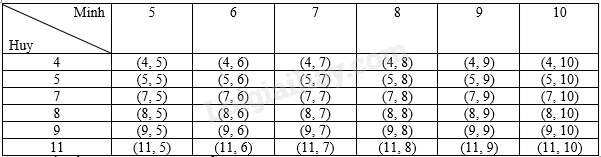
Giải bài tập 8.17 trang 66 SGK Toán 9 tập 2 - Kết nối tri thứcHai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn thì sẽ là người thắng cuộc. Nếu hai số được chọn bằng nhau thì kết quả là hòa. Tính xác suất của các biến cố sau: a) A: “Bạn Minh thắng”; b) B: “Bạn Huy thắng”. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn thì sẽ là người thắng cuộc. Nếu hai số được chọn bằng nhau thì kết quả là hòa. Tính xác suất của các biến cố sau: a) A: “Bạn Minh thắng”; b) B: “Bạn Huy thắng”. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Cách tính xác suất của một biến cố E: Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu . Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng. Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E. Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu . Lời giải chi tiết Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số Huy và Minh chọn. Ta có bảng miêu tả không gian mẫu là:
Do đó, số phần tử của không gian mẫu là 36. Vì Minh và Huy chọn ngẫu nhiên một số nên các kết quả có thể xảy ra ở trên là đồng khả năng. Có 17 kết quả thuận lợi của biến cố A là: (4, 5), (4, 6), (4, 7), (4, 8), (4, 9), (4, 10), (5, 6), (5, 7), (5, 8), (5, 9), (5, 10), (7, 8), (7, 9), (7, 10), (8, 9), (8, 10), (9, 10). Do đó, . Có 15 kết quả thuận lợi của biến cố B là: (7, 5), (7, 6), (8, 5), (8, 6), (8, 7), (9, 5), (9, 6), (9, 7), (9, 8), (11, 5), (11, 6), (11, 7), (11, 8), (11, 9), (11, 10). Do đó, .
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|