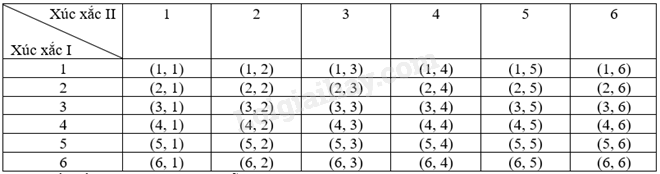
Giải bài tập 8.10 trang 65 SGK Toán 9 tập 2 - Kết nối tri thứcGieo đồng thời hai con xúc xắc cân đối và đồng chất I và II. Tính xác suất của các biến cố sau: G: “Không có con xúc xắc xuất hiện mặt 6 chấm”; H: “Số chấm xuất hiện trên con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”; K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Gieo đồng thời hai con xúc xắc cân đối và đồng chất I và II. Tính xác suất của các biến cố sau: G: “Không có con xúc xắc xuất hiện mặt 6 chấm”; H: “Số chấm xuất hiện trên con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”; K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Cách tính xác suất của một biến cố E: Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu Ω. Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng. Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E. Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu Ω. Lời giải chi tiết Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II. Ta có bảng miêu tả không gian mẫu là:
Do đó, số phần tử của không gian mẫu Ω là 36. Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng. Có 25 kết quả thuận lợi của biến cố G là: (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (1, 5), (2, 5), (3, 5), (4, 5), (5, 5). Do đó, P(G)=2536. Có 6 kết quả thuận lợi của biến cố H là: (1, 5), (1, 6), (3, 5), (3, 6), (5, 5), (5, 6) nên P(H)=636=16. Có 16 kết quả thuận lợi của biến cố K là: (3, 3), (4, 3), (5, 3), (6, 3), (3, 4), (4, 4), (5, 4), (6, 4), (3, 5), (4, 5), (5, 5), (6, 5), (3, 6), (4, 6), (5, 6), (6, 6). Do đó, P(K)=1636=49.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|