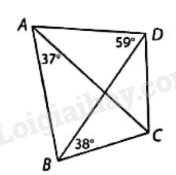
Giải bài tập 7.27 trang 40 SGK Toán 9 tập 2 - Cùng khám phá

Đề bài

Cho ABCD là tứ giác nội tiếp có $\widehat {BAC} = {37^o},\widehat {ADB} = {59^o}$ và $\widehat {CBD} = {38^o}$. Số đo của góc ADC bằng

A. 75$^o$

B. 96$^o$

C. 97$^o$

D. 87$^o$

Lời giải chi tiết

Ta có: $\widehat {BDC} = \widehat {BAC} = {37^o}$ (hai góc nội tiếp cùng chắn cung BC)

Suy ra $\widehat {ADC} = \widehat {ADB} + \widehat {BDC} = {59^o} + {37^o} = {96^o}$

Chọn đáp án B.