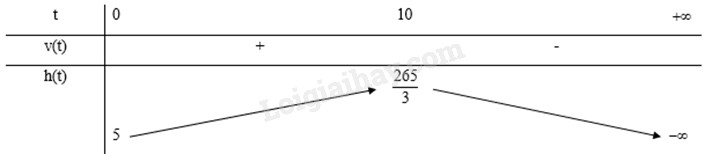
Giải bài tập 7 trang 16 SGK Toán 12 tập 2 - Cánh diều

Đề bài

Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số

\(v(t) =  - 0,1{t^3} + {t^2}\)

Trong đó t tính theo tuần, v(t) tính bằng cm/tuần. Gọi h(t) (tính bằng cm) là độ cao của cây cà chua ở tuần thứ t

a) Viết công thức xác định hàm số h(t) \((t \ge 0)\)

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây cà chua đó là bao nhiêu?

d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao bao nhiêu?

Lời giải chi tiết

a) \(h(t) = \int {v(t)dt = } \int {\left( { - 0,1{t^3} + {t^2}} \right)} dt =  - 0,025{t^4} + \frac{{{t^3}}}{3} + C\)\((t \ge 0)\)

\(h(0) =  - 0,{025.0^4} + \frac{{{0^3}}}{3} + C = 5 \Rightarrow C = 5\)

Vậy \(h(t) =  - 0,025{t^4} + \frac{{{t^3}}}{3} + 5\)

b) Xét hàm số \(h(t) =  - 0,025{t^4} + \frac{{{t^3}}}{3} + 5\)

\(h'(t) = v(t) =  - 0,1{t^3} + {t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0(nghiem\;kep)\\x = 10\end{array} \right.\)

Bảng biển thiên:

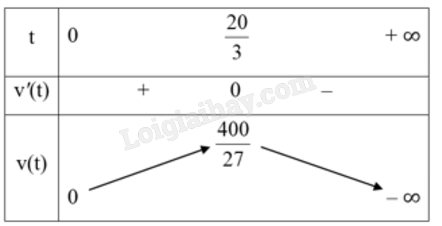
Từ bảng biến thiên ta thấy, giai đoạn tăng trưởng của cây cà chua đó kéo dài 10 tuần

c) Từ bảng biến thiên ta thấy, chiều cao tối đa của cây cà chua đó là \(\frac{{265}}{3}\) cm

d) Xét \(v(t) =  - 0,1{t^3} + {t^2}\)

\(v'(t) =  - 0,3{t^2} + 2t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \frac{{20}}{3}\end{array} \right.\)

Bảng biển thiên:

Từ bảng biến thiên ta thấy, vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua sẽ cao \(\frac{{400}}{{27}}\)cm