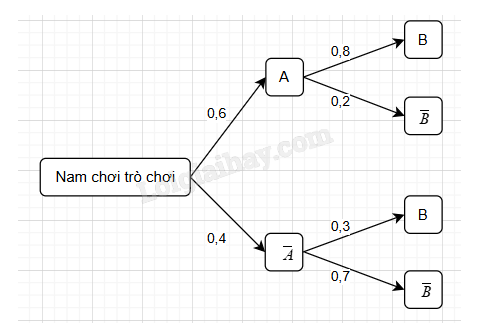
Giải bài tập 6.7 trang 101 SGK Toán 12 tập 2 - Cùng khám pháBạn Nam tham gia một gian hàng trò chơi dân gian trong hội xuân của trường. Trò chơi có hai lượt chơi. Xác suất để Nam thắng ở lượt chơi thứ nhất là 0,6. Nếu Nam thắng ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,8. Ngược lại, nếu Nam thua ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,3. a) Vẽ sơ đồ hình cây mô tả các khả năng xảy ra và xác suất tương ứng khi Nam tham gia trò chơi này. b) Biết Nam đã thắng ở lượt chơi thứ hai, tính xác suất Nam th Đề bài Bạn Nam tham gia một gian hàng trò chơi dân gian trong hội xuân của trường. Trò chơi có hai lượt chơi. Xác suất để Nam thắng ở lượt chơi thứ nhất là 0,6. Nếu Nam thắng ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,8. Ngược lại, nếu Nam thua ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,3. a) Vẽ sơ đồ hình cây mô tả các khả năng xảy ra và xác suất tương ứng khi Nam tham gia trò chơi này. b) Biết Nam đã thắng ở lượt chơi thứ hai, tính xác suất Nam thắng ở lượt chơi thứ nhất. Phương pháp giải - Xem chi tiết a) - Biểu diễn các khả năng thắng/thua của Nam trong hai lượt chơi. - Xác suất tương ứng được tính từ dữ kiện bài toán. b) Tính xác suất Nam thắng lượt thứ nhất khi biết Nam thắng lượt thứ hai: \(P(A|B) = \frac{{P(B|A) \cdot P(A)}}{{P(B)}}\) trong đó: - \(A\): Biến cố Nam thắng ở lượt thứ nhất. - \(B\): Biến cố Nam thắng ở lượt thứ hai. Sử dụng công thức tính xác suất toàn phần để tính \(P(B)\) (Nam thắng ở lượt thứ hai): \(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A)\) Lời giải chi tiết a) Gọi: - \(A\): Biến cố Nam thắng ở lượt thứ nhất. - \(B\): Biến cố Nam thắng ở lượt thứ hai. Sơ đồ hình cây mô tả các khả năng và xác suất tương ứng như sau:
- \(P(A) = 0,6\), \(P(\bar A) = 0,4\). - Nếu \(A\) (Nam thắng lượt thứ nhất): \(P(B|A) = 0,8\), \(P(\bar B|A) = 0,2\). - Nếu \(\bar A\) (Nam thua lượt thứ nhất): \(P(B|\bar A) = 0,3\), \(P(\bar B|\bar A) = 0,7\). b) * Tính \(P(B)\) bằng công thức xác suất toàn phần: \(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A).\) \(P(B) = (0,8 \cdot 0,6) + (0,3 \cdot 0,4) = 0,48 + 0,12 = 0,6.\) * Tính \(P(A|B)\) bằng định lý Bayes: \(P(A|B) = \frac{{P(B|A) \cdot P(A)}}{{P(B)}}.\) \(P(A|B) = \frac{{0,8 \cdot 0,6}}{{0,6}} = 0,8.\)
|