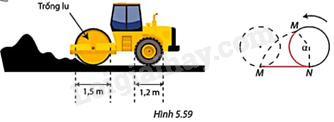
Giải bài tập 5.29 trang 122 SGK Toán 9 tập 1 - Cùng khám phá

Đề bài

Một chiếc xe lu có đường kính trống lu là 1,5m và đường kính của bánh sau là 1,2m (Hình 5.59). Khi hoạt động, trống lu quay hết một vòng $\left( {{{360}^o}} \right)$ trong 5 phút.

a) Trong mỗi phút, trống lu quay được bao nhiêu độ và xe lu cán được bao nhiêu mét đường?

b) Để cán được 1 mét đường thì trống lu phải quay một góc bao nhiêu độ?

c) Để trống lu quay được 1 vòng thì bánh sau phải quay bao nhiêu vòng?

Lời giải chi tiết

a) Bán kính trống lu là:

$\frac{{1,5}}{2} = 0,75\left( m \right)$.

Trong một phút, trống lu quay được $\frac{{{{360}^o}}}{5} = {72^o}$.

Trong một phút, lu xe cán được số mét đường là:

$l = \frac{{\pi .0,75.72}}{{180}} = \frac{{3\pi }}{{10}}\left( m \right)$.

b) Trống lu cán được 1m đường thì ta có:

$1 = \frac{{\pi .0,75n}}{{180}}$, suy ra: $n = \frac{{240}}{\pi }$.

Vậy để cán được 1 mét đường thì trống lu phải quay thì trống lu phải quay một góc $\frac{{240}}{\pi } \approx {76^o}$.

c) Độ dài đường tròn đường kính 1,5m là:

${C_1} = 1,5\pi \left( {cm} \right)$.

Độ dài đường tròn đường kính 1,2m là:

${C_2} = 1,2\pi \left( {cm} \right)$.

Ta có: $\frac{{{C_1}}}{{{C_2}}} = \frac{{1,5\pi }}{{1,2\pi }} = 1,25$.

Vậy khi trống lu quay được 1 vòng thì bánh sau xe quay được 1,25 vòng.