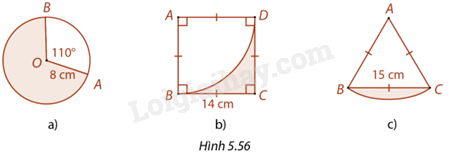
Giải bài tập 5.26 trang 121 SGK Toán 9 tập 1 - Cùng khám phá

Đề bài

Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.

Lời giải chi tiết

a) Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung AB nhỏ là bằng 110 độ.

Khi đó, số đo cung AB lớn bằng:

${360^o} - {110^o} = {250^o}$.

Phần được tô màu là hình quạt tâm O, cung lớn AB nên

+ Diện tích phần tô màu là:

$S = \frac{{\pi {{.8}^2}.250}}{{360}} = \frac{{400\pi }}{9} \approx 139,6\left( {c{m^2}} \right)$

+ Độ dài cung AB lớn là:

${l_{AB}} = \frac{{\pi .8.250}}{{180}} = \frac{{100\pi }}{9}\left( {cm} \right)$

+ Chu vi hình được tô màu là:

$C = OA + OB + {l_{AB}} = 8 + 8 + \frac{{100\pi }}{9} = 16 + \frac{{100\pi }}{9} \approx 50,9\left( {cm} \right)$

b) Diện tích hình vuông ABCD là:

${S_{ABCD}} = {14^2} = 196\left( {c{m^2}} \right)$

Phần không tô màu là $\frac{1}{4}$ hình tròn bán kính 14cm nên diện tích phần không tô màu là: ${S_1} = \frac{1}{4}{.5^2}.\pi  = \frac{{25}}{4}\pi \left( {c{m^2}} \right)$.

Diện tích phần tô màu là:

$S = {S_{ABCD}} - {S_1} = 196 - \frac{{25\pi }}{4} \approx 176,4\left( {c{m^2}} \right)$

Độ dài cung BD là:

${l_{BD}} = \frac{{\pi .14.90}}{{180}} = 7\pi \left( {cm} \right)$

Chu vi phần được tô màu là:

$C = DC + CB + {l_{BD}} = 14 + 14 + 7\pi  = 28 + 7\pi  \approx 50\left( {cm} \right)$

c) Tam giác ABC có: $AB = BC = CA$ nên tam giác ABC đều. Do đó, $\widehat {BAC} = {60^o}$ nên hình quạt tâm A, hai bán kính AB, AC có số đo cung BC bằng 60 độ.

Diện tích hình quạt tâm A, cung BC là:

${S_q} = \frac{{\pi {{.15}^2}.60}}{{360}} = \frac{{75\pi }}{2}\left( {c{m^2}} \right)$

Diện tích tam giác đều ABC cạnh 15cm là:

${S_{ABC}} = \frac{{{{15}^2}\sqrt 3 }}{4} = \frac{{225\sqrt 3 }}{4}\left( {c{m^2}} \right)$

Do đó, diện tích phần được tô màu là:

$S = {S_q} - {S_{ABC}} = \frac{{75\pi }}{2} - \frac{{225\sqrt 3 }}{4} \approx 20,4\left( {c{m^2}} \right)$

Độ dài cung BC là:

${l_{BC}} = \frac{{\pi .15.60}}{{180}} = 5\pi \left( {cm} \right)$.

Chu vi phần được tô màu là:

${l_{BC}} + BC = 5\pi  + 15 \approx 30,7\left( {cm} \right)$.