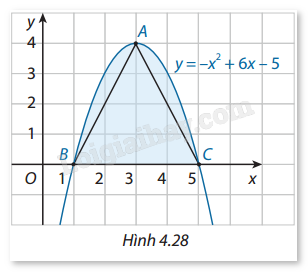
Giải bài tập 4.22 trang 31 SGK Toán 12 tập 2 - Cùng khám phá

Đề bài

Gọi $(H)$ là hình phẳng giới hạn bởi parabol $y =  - {x^2} + 6x - 5$ và trục hoành. (Hình 4.28)

a) Tính diện tích $S$ của hình $(H)$.

b) Từ thế kỉ thứ III trước Công nguyên, khi phép tính tích phân chưa ra đời, Archimedes đã dùng phương pháp của riêng mình và chỉ ra rằng diện tích của hình $(H)$ bằng $\frac{4}{3}$ lần diện tích tam giác $ABC$. Tính $S$ theo kết quả mà Archimedes đã tìm ra và so sánh với kết quả ở câu a.

Lời giải chi tiết

a)

- Phương trình parabol là:

$y =  - {x^2} + 6x - 5.$

- Tìm nghiệm của phương trình $y = 0$:

$- {x^2} + 6x - 5 = 0\quad  \Rightarrow \quad x = 1,{\mkern 1mu} x = 5.$

- Diện tích hình phẳng $S$ được tính bằng tích phân:

$S = \int_1^5 {( - {x^2} + 6x - 5)} {\mkern 1mu} dx.$

Tính tích phân:

$S = \left[ { - \frac{{{x^3}}}{3} + 3{x^2} - 5x} \right]_1^5 = \left( { - \frac{{125}}{3} + 50} \right) - \left( { - \frac{1}{3} - 2} \right) = \frac{{32}}{3}.$

Vậy diện tích hình phẳng $S = \frac{{32}}{3}$.

b)

- Diện tích tam giác $ABC$ với $A(3,4)$, $B(1,0)$, và $C(5,0)$ là:

${S_{\Delta ABC}} = \frac{1}{2} \times 4 \times 4 = 8.$

- Theo Archimedes, diện tích hình $(H)$ bằng $\frac{4}{3}$ lần diện tích tam giác $ABC$:

$S = \frac{4}{3} \times 8 = \frac{{32}}{3}.$

Kết quả này khớp với kết quả của câu a.