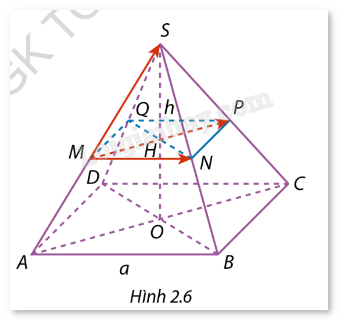
Giải bài tập 2.2 trang 54 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

Cho hình chóp đều S.ABCD có cạnh đáy

$a$ và đường cao $h$. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6).

a) Trong những vectơ khác $\vec O$, có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ:

- Cùng hướng với $\overrightarrow {MN}$;

- Bằng $\overrightarrow {MN}$.

b) Tìm độ dài các vectơ $\overrightarrow {MP} ,\overrightarrow {MS}$ theo $a$ và $h$.

Lời giải chi tiết

a) Liệt kê các vectơ

- Cùng hướng với $\overrightarrow {MN}$:

Vectơ cùng hướng với $\overrightarrow {MN}$ là các vectơ có phương và chiều giống với $\overrightarrow {MN}$, cụ thể là: $\overrightarrow {QP}$, $\overrightarrow {AB}$, $\overrightarrow {DC}$.

- Bằng $\overrightarrow {MN}$:

Vectơ bằng $\overrightarrow {MN}$ là các vectơ có độ dài và phương chiều giống với $\overrightarrow {MN}$, cụ thể là: $\overrightarrow {QP}$

b) Tính độ dài các vectơ $\overrightarrow {MP} ,\overrightarrow {MS}$

- Tính độ dài $\overrightarrow {MP}$:

Ta xét tam giác đều SAC có MP là đường trung bình của tam giác đều SAC

$MP = \frac{1}{2}AC = \frac{1}{2} \cdot a\sqrt 2$ (AC là đường chéo của hình vuông ABCD)

Do đó: $\overrightarrow {MP}  = \frac{{a\sqrt 2 }}{2}$

- Tính độ dài $\overrightarrow {MS}$:

Ta xét tam giác vuông SOA với $O$ là tâm của hình vuông đáy ABCD:

$SA = \sqrt {{h^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = \sqrt {{h^2} + \frac{{{a^2}}}{2}}$

Vì $M$ là trung điểm của SA, ta có: $SM = \frac{1}{2}SA = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}}$

Do đó: $\overrightarrow {MS}  = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}}$