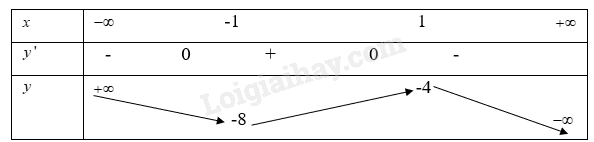
Giải bài tập 1.4 trang 9 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

a) $y =  - {x^3} + 3x - 6$

b) $y = \frac{{x - 1}}{{x + 2}}$

c) $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$

d) $y = \frac{{3x}}{{{x^2} - 9}}$

Lời giải chi tiết

a)  $y =  - {x^3} + 3x - 6$

Hàm số xác định trên R

Ta có: $y' =  - 3{x^2} + 3$

Xét $y' = 0$ $\Rightarrow  - 3{x^2} + 3 = 0$

$\Rightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.$

Từ đó ta có bảng biến thiên là

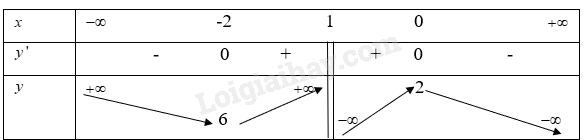
Từ bảng biến thiên ta có:

Hàm số $y =  - {x^3} + 3x - 6$ đồng biến trên khoảng$( - 1;1)$

Hàm số $y =  - {x^3} + 3x - 6$ nghịch biến trên khoảng$( - \infty ; - 1),(1; + \infty )$

Hàm số $y =  - {x^3} + 3x - 6$ đạt giá trị cực đại $x = 1$tại khi đó$y =  - 4$

Hàm số $y =  - {x^3} + 3x - 6$ đạt giá trị cực tiểu tại $x =  - 1$ khi đó$y =  - 8$

b) $y = \frac{{x - 1}}{{x + 2}}$

Hàm số trên xác định trên R/{2}

Ta có: $y' = \frac{3}{{{{(x + 2)}^2}}}$

Vì $y' = \frac{3}{{{{(x + 2)}^2}}} > 0$với $\forall x \in R/\{  - 2\}$

Nên hàm số $y = \frac{{x - 1}}{{x + 2}}$ đồng biến trên khoảng $( - \infty ;2),(2; + \infty )$

Và hàm số $y = \frac{{x - 1}}{{x + 2}}$ không có điểm cực trị

c)  $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$

Hàm số xác định trên R/{-1}

Ta có: $y' = \frac{{( - 2x + 2)(x + 1) - ( - {x^2} + 2x + 2)}}{{{{(x + 1)}^2}}}$

$= \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}$

Xét $y' = 0$$\Rightarrow  - {x^2} - 2x = 0$

$\Rightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.$

Từ đó ta có bảng biến thiên là

Từ bảng biến thiên, ta có:

Hàm số $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$ đồng biến trên khoảng$( - 2;1),(1;2)$

Hàm số $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$ nghịch biến trên khoảng$( - \infty ; - 2),(0; + \infty )$

Hàm số $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$ đạt giá trị cực đại $x = 0$ tại khi đó $y = 2$

Hàm số $y = \frac{{ - {x^2} + 2x + 2}}{{x + 1}}$ đạt giá trị cực tiểu tại $x =  - 2$ khi đó $y = 6$

d) $y = \frac{{3x}}{{{x^2} - 9}}$

Hàm số trên xác định trên R/{-3;3}

Ta có: $y' = \frac{{3({x^2} - 9) - 3x.2x}}{{{{({x^2} - 9)}^2}}}$ $= \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}}$

Vì $y' = \frac{{ - 3{x^2} - 27}}{{{{({x^2} - 9)}^2}}} < 0$ với $\forall x \in R/\{  - 3;3\}$

Nên hàm số $y = \frac{{3x}}{{{x^2} - 9}}$ nghịch biến trên khoảng$( - \infty ; - 3),( - 3;3),(3; + \infty )$

Và hàm số$y = \frac{{3x}}{{{x^2} - 9}}$ không có cực trị