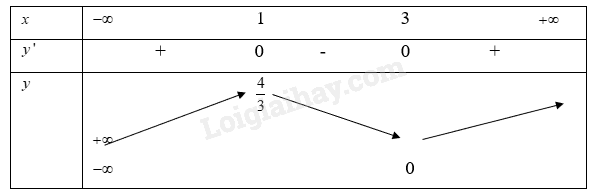
Giải bài tập 1.3 trang 9 SGK Toán 12 tập 1 - Cùng khám pháa) (y = frac{x}{3}{(x - 3)^2}) b) (y = left| x right|) c) (y = {3^{x - 2{x^2}}}) d) (y = ln ({x^2} + e)) Đề bài a) \(y = \frac{x}{3}{(x - 3)^2}\) b) \(y = \left| x \right|\) c) \(y = {3^{x - 2{x^2}}}\) d) \(y = \ln ({x^2} + e)\) Phương pháp giải - Xem chi tiết Bước 1: Tính \(y'\) Bước 2: Lập bảng biến thiên Bước 3: Xác định cực trị của hàm số dựa vào bảng biến thiên Lời giải chi tiết a) \(y = \frac{x}{3}{(x - 3)^2}\) Hàm số trên xác định trên R Ta có: \(y' = \frac{{{{(x - 3)}^2}}}{3} + \frac{{x.2(x - 3)}}{3}\) \( = \frac{{3{x^2} - 12x + 9}}{3}\) \( = {x^2} - 4x + 3 = (x - 3)(x - 1)\) Xét \(y' = 0\) \( \Rightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\) Ta có bảng biến thiên:
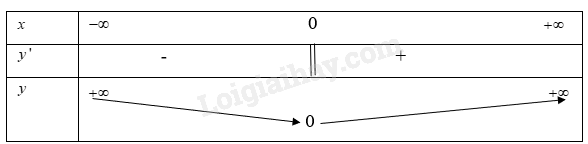
Từ bảng biến thiên ta có Hàm số đạt giá trị cực đại tại \(x = 1\)khi đó\(y = \frac{4}{3}\) Hàm số đạt giá trị cực tiểu tại \(x = 3\)khi đó \(y = 0\) b) \(y = \left| x \right|\) Hàm số trên xác định trên R \(y = \left| x \right|\)\( = \sqrt {{x^2}} \) Ta có: \(y' = \frac{{2x}}{{2\sqrt {{x^2}} }} = \frac{x}{{\sqrt {{x^2}} }}\) Vì \(\sqrt {{x^2}} > 0\)nên dấu của \(y'\)cũng là dấu của \(x\) Khi đó ta có bảng biến thiên
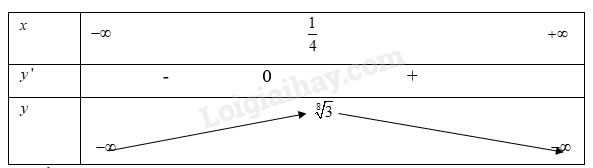
Từ bảng biến thiên ta có Hàm số trên đạt giá trị cực tiểu tại \(x = 0\) khi đó \(y = 0\) c) \(y = {3^{x - 2{x^2}}}\) Hàm số trên xác định trên R Ta có: \(y' = {3^{x - 2{x^2}}}(1 - 4x)\) Xét \(y' = 0\)\( \Rightarrow 1 - 4x = 0\) \( \Rightarrow x = \frac{1}{4}\) Ta có bảng biến thiên
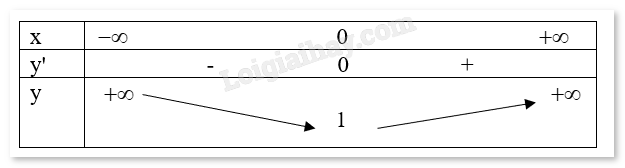
Từ bảng biến thiên ta có Hàm số trên đạt giá trị cực tiểu tại\(x = \frac{1}{4}\)khi đó \(y = \sqrt[8]{3}\) d) \(y = \ln ({x^2} + e)\) Hàm số trên xác định trên R Ta có: \(y' = \frac{{2x}}{{{x^2} + e}}\) Xét \(y' = 0\)\( \Rightarrow x = 0\) Ta có bảng biến thiên
Từ bảng biến thiên ta có: Hàm số trên đạt giá trị cực tiểu tại \(x = 0\)khi đó \(y = 1\)
|