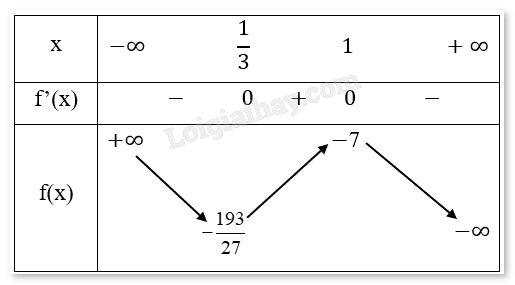
Giải bài tập 1.30 trang 45 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

Lập bảng biến thiên, tìm khoảng đơn điệu và cực trị (nếu có) của hàm số:

a) $y =  - {x^3} + 2{x^2} - x - 7$

b) $y = \frac{{x - 6}}{{1 - 2x}}$

c) $y = \sqrt {4x - {x^2}}$

Lời giải chi tiết

a)

- Tập xác định: D = R.

- Sự biến thiên:

Giới hạn:

$\mathop {\lim }\limits_{x \to  + \infty } f(x) = \mathop {\lim }\limits_{x \to  + \infty } \left( { - {x^3} + 2{x^2} - x - 7} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} + \frac{1}{{{x^2}}} + \frac{7}{{{x^3}}}} \right)} \right] =  - \infty$

$\mathop {\lim }\limits_{x \to  - \infty } f(x) = \mathop {\lim }\limits_{x \to  - \infty } \left( { - {x^3} + 2{x^2} - x - 7} \right) = \mathop {\lim }\limits_{x \to  - \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} + \frac{1}{{{x^2}}} + \frac{7}{{{x^3}}}} \right)} \right] =  + \infty$

_{Ta có:} ${y^\prime } =  - 3{x^2} + 4x - 1$

${y^\prime } = 0 \leftrightarrow  - 3{x^2} + 4x - 1 = 0 \leftrightarrow x = 1{\rm{  }}$hoặc $x = \frac{1}{3}$

Bảng biến thiên:

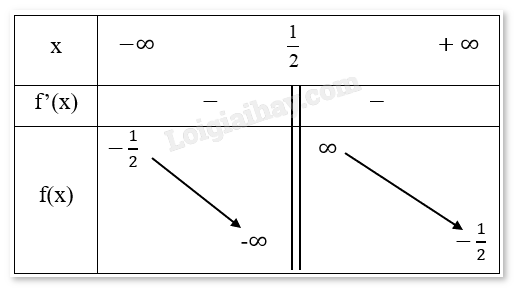
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,$\frac{1}{3}$) và (1,∞), đồng biến trên khoảng ($\frac{1}{3}$,1).

Cực trị: Hàm số đạt cực tiểu tại $x = \frac{1}{2},{y_{CT}} =  - \frac{{193}}{{27}}$

Hàm số đạt cực đại tại $x = 1,{y_{CD}} =  - 7$

b)

- Tập xác định: ${\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{1}{2}} \right\}$.

- Sự biến thiên:

Giới hạn, tiệm cận:

$\mathop {\lim }\limits_{x \to  + \infty } f(x) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x - 6}}{{1 - 2x}} =  - \frac{1}{2}$

$\mathop {\lim }\limits_{x \to  - \infty } f(x) = \mathop {\lim }\limits_{x \to  - \infty } \frac{{x - 6}}{{1 - 2x}} =  - \frac{1}{2}$

Suy ra đường thẳng ${\rm{y}} =  - \frac{1}{2}$ là đường tiệm cận ngang của đồ thị hàm số đã cho.

$\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} \frac{{x - 6}}{{1 - 2x}} =  + \infty$

$\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} \frac{{x - 6}}{{1 - 2x}} =  - \infty$

Suy ra đường thẳng ${\rm{x}} = \frac{1}{2}$. là đường tiệm cận đứng của đồ thị hàm số đã cho.

Ta có: ${y^\prime } = \frac{{ - 11}}{{{{(1 - 2x)}^2}}} < 0$

Suy ra hàm số nghịch biến trên tập xác định.

Bảng biến thiên:

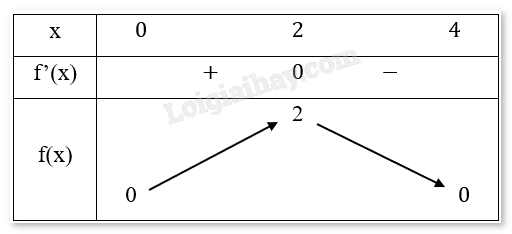
Chiều biến thiên: Hàm số nghịch biến trên $\left( { - \infty ,\frac{1}{2}} \right)$. và $\left( {\frac{1}{2}, + \infty } \right)$.

Cực trị: Hàm số không có cực trị.

c)

- Tập xác định: D = [0,4].

- Đạo hàm: $f'(x) = \frac{{4 - 2x}}{{2\sqrt {4x - {x^2}} }} = \frac{{2 - x}}{{\sqrt {4x - {x^2}} }}$

- Giải phương trình $f'(x) = 0$:

$\begin{array}{l}\frac{{2 - x}}{{\sqrt {4x - {x^2}} }} = 0\\ \Rightarrow 2 - x = 0\\ \Leftrightarrow x = 2\end{array}$

- Bảng biến thiên:

- Chiều biến thiên: Hàm số đồng biến trên khoảng [0,2) và nghịch biến trên khoảng (2,4].

- Hàm số đạt cực đại tại  và không có cực tiểu.