Giải bài tập 1.32 trang 45 SGK Toán 12 tập 1 - Cùng khám pháTrong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu? Đề bài Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu?
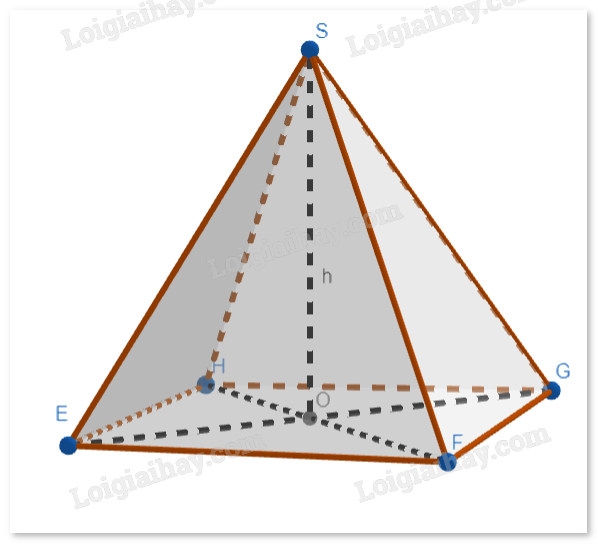
Phương pháp giải - Xem chi tiết - Đặt x là độ dài các cạnh của hình vuông EFGH. - Tính diện tích của hình vuông EFGH theo x. - Tìm chiều cao từ đỉnh S xuống đáy. - Tìm hàm thể tích và khảo sát. Lời giải chi tiết Theo đề bài ta có hình vẽ như sau:
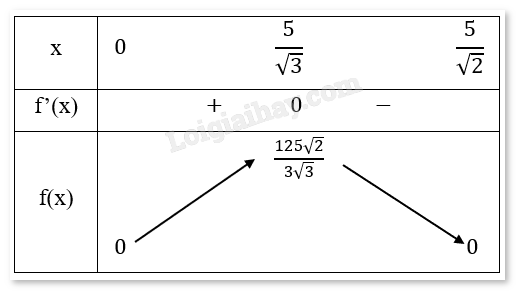
- Đặt x (cm) là độ dài các cạnh của hình vuông EFGH (x∈\((0;2,5\sqrt 2 )\)). Tương đương EF=FG=GH=EH=x nên \({S_{EFGH}} = {x^2}\) Đặt SO là chiều cao của hình chóp S.EFGH. - Độ dài đường chéo của hình vuông EFGH là \(HF = EG = \sqrt {{x^2} + {x^2}} = x\sqrt 2 \)cm. - Ta có: \(SE = AE = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{5 - x\sqrt 2 }}{2}} \right)}^2}} = \sqrt {2.{{\left( {\frac{5}{2}} \right)}^2} - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 2{x^2}} \) - Vì tam giác vuông SOE vuông tại O nên suy ra: \(SO = \sqrt {S{E^2} - E{O^2}} = \sqrt {\frac{1}{4}(50 - 2{x^2}) - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 4{x^2}} \) - Thể tích của hình chóp S.EFGH là: \({V_{S.EFGH}} = \frac{1}{3}.{S_{EFGH}}.SO = \frac{1}{3}.{x^2}.\frac{1}{2}\sqrt {50 - 4{x^2}} = \frac{1}{6}{x^2}\sqrt {50 - 4{x^2}} \) Để thể tích hình chóp S.EFGH là lớn nhất thì \(f(x) = {x^2}\sqrt {50 - 4{x^2}} \) phải đạt giá trị lớn nhất trong khoảng từ \((0;2,5\sqrt 2 )\). - Tính đạo hàm: \(f'(x) = 2x\sqrt {50 - 4{x^2}} + {x^2}.\frac{{ - 4x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{ - 12{x^3} + 100x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{4x(3{x^2} - 25)}}{{\sqrt {50 - 4{x^2}} }}\) - Giải phương trình \(f'(x) = 0\) \[4x(3{x^2} - 25) = 0 \Leftrightarrow {x_1} = 0,{x_2} = \frac{5}{{\sqrt 3 }},{x_3} = - \frac{5}{{\sqrt 3 }}\](loại \({x_1},{x_3}\) vì x > 0). - Bảng biến thiên:
Nhận thấy \(f(x)\) sẽ đạt giá trị lớn nhất tại \(x = \frac{5}{{\sqrt 3 }}\) Vậy thể tích lớn nhất của khối chóp tứ giác đều tạo thành là \(V = \frac{1}{6}.{\left( {\frac{5}{{\sqrt 3 }}} \right)^2}.\sqrt {50 - 4{{\left( {\frac{5}{{\sqrt 3 }}} \right)}^2}} \approx 5,67c{m^3}\).
|