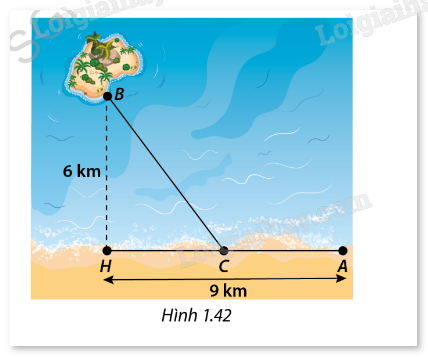
Giải bài tập 1.28 trang 36 SGK Toán 12 tập 1 - Cùng khám pháMột công ty muốn làm một đường ống dẫn từ vị trí A trên bờ biển đến vị trí B trên hòn đảo. Khoảng cách từ điểm B đến bờ biển là BH=6 km (Hình 1.42). Giá tiền để xây dựng đường ống trên bờ là 50.000 USD mỗi kilomet và giá tiền xây dựng đường ống trên biển là 130.000 USD mỗi kilomet, biết rằng AH=9 km. Xác định vị trí điểm C trên đoạn AH để khi lắp ống dẫn theo đường gấp khúc ACB thì chi phí công ty bỏ ra là thấp nhất. Đề bài Một công ty muốn làm một đường ống dẫn từ vị trí A trên bờ biển đến vị trí B trên hòn đảo. Khoảng cách từ điểm B đến bờ biển là BH=6 km (Hình 1.42). Giá tiền để xây dựng đường ống trên bờ là 50.000 USD mỗi kilomet và giá tiền xây dựng đường ống trên biển là 130.000 USD mỗi kilomet, biết rằng AH=9 km. Xác định vị trí điểm C trên đoạn AH để khi lắp ống dẫn theo đường gấp khúc ACB thì chi phí công ty bỏ ra là thấp nhất.
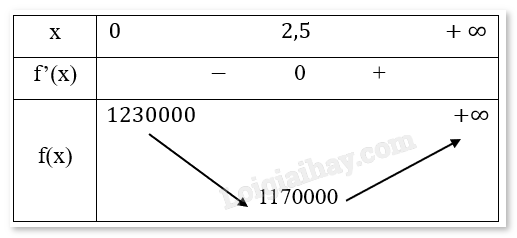
Phương pháp giải - Xem chi tiết - Đặt HC = 𝑥 và tính đoạn CB. - Tính tổng chi phí xây dựng đường ống trên bờ và trên biển và thiết lập hàm chi phí theo 𝑥. - Tìm giá trị tối thiểu bằng cách khảo sát hàm chi phí theo 𝑥. Lời giải chi tiết - Đặt HC = 𝑥. Khi đó, AC = 9 – 𝑥. (0≤𝑥≤9) \(CB = \sqrt {{x^2} + {6^2}} = \sqrt {{x^2} + 36} \) - Chi phí xây dựng đường ống trên bờ: \(50.000 \times (9 - x)\) - Chi phí xây dựng đường ống trên biển: \(130.000 \times \sqrt {{x^2} + 36} \) - Tổng chi phí: \(50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} \) 3. Tìm giá trị tối thiểu: - Đặt hàm chi phí: \(f(x) = 50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} \) - Lấy đạo hàm của hàm chi phí: \({f^\prime }(x) = - 50.000 + 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }}\) - Giải phương trình \({f^\prime }(x) = 0\): \(\begin{array}{l} - 50.000 + 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }} = 0\\ \Leftrightarrow 130.000 \times \frac{x}{{\sqrt {{x^2} + 36} }} = 50.000\\ \Leftrightarrow \frac{x}{{\sqrt {{x^2} + 36} }} = \frac{5}{{13}}\\ \Leftrightarrow 13x = 5\sqrt {{x^2} + 36} \\ \Leftrightarrow 169{x^2} = 25({x^2} + 36)\\ \Leftrightarrow 169{x^2} = 25{x^2} + 900\\ \Leftrightarrow 144{x^2} = 900\\ \Leftrightarrow x = \pm 2.5\end{array}\) Loại x=−2.5 vì x ≥0 \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} [50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} ] = 1230000\) \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } [50.000 \times (9 - x) + 130.000 \times \sqrt {{x^2} + 36} ] = \infty \) - Bảng biến thiên:
Vậy khi điểm C cách điểm H 1 khoảng là 2,5km thì chi phí công ty bỏ ra để lắp ống dẫn theo đường gấp khúc ACB là nhỏ nhất.
|