Giải bài tập 12 trang 48 SGK Toán 12 tập 1 - Cánh diềuMột bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông? Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài
Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông? Phương pháp giải - Xem chi tiết Phân tích đề bài. Tìm các mối quan hệ trong bài. Lập phương trình và giải. Lời giải chi tiết
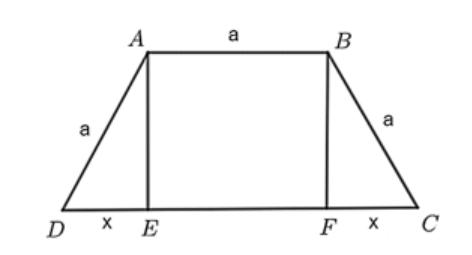
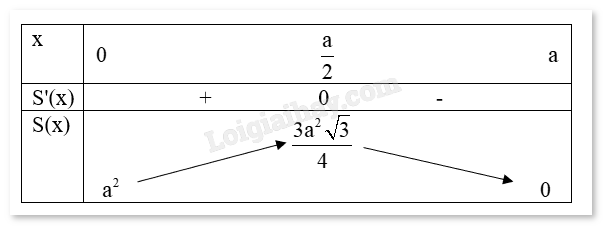
Dựng các đường cao AE và BF của hình thang cân ABCD như hình vẽ trên. Vì ABCD là hình thang cân nên DE = FC và EF = AB = a. Đặt DE = FC = x (m) (x > 0). Ta có DC = DE + EF + FC = x + a + x = 2x + a. Theo định lí Pythagore, ta suy ra \(AE = \sqrt {A{D^2} - D{E^2}} = \sqrt {{a^2} - {x^2}} \) (m). Rõ ràng, x phải thỏa mãn điều kiện 0 < x < a. Diện tích của hình thang cân ABCD là: \(S = \frac{1}{2}(AB + CD)AE = \frac{1}{2}(a + 2x + a)\sqrt {{a^2} - {x^2}} = (a + x)\sqrt {{a^2} - {x^2}} \) (m2). Xét hàm số \(S(x) = (a + x)\sqrt {{a^2} - {x^2}} \) với \(x \in (0;a)\). Ta có \(S'(x) = \frac{{ - 2{x^2} - ax + {a^2}}}{{\sqrt {{a^2} - {x^2}} }} = 0 \Leftrightarrow - 2{x^2} - ax + {a^2} = 0 \Leftrightarrow (x + a)(a - 2x) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - a}\\{x = \frac{a}{2}}\end{array}} \right.\) Khi đó trên khoảng (0;a), S’(x) = 0 khi \(x = \frac{a}{2}\). Ta có bảng biến thiên:
Căn cứ vào bảng biến thiên, ta thấy hàm số S(x) đạt giá trị lớn nhất bằng \(\frac{{3{a^2}\sqrt 3 }}{4}\) tại \(x = \frac{a}{2}\). Vậy bác đó có thể rào được mảnh vườn có diện tích lớn nhất là \(\frac{{3{a^2}\sqrt 3 }}{4}\) (m2).
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|